Упражнения. 1. По какому закону распределена случайная величина Х, если плотность вероятностей этой величины определена функцией при при

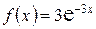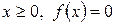1. По какому закону распределена случайная величина Х, если плотность вероятностей этой величины определена функцией при при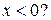

2. Найти среднее квадратическое отклонение случайной величины Х
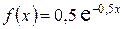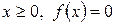с плотностью распределения при при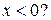

3. Найти функцию распределения случайной величины Х, если ее плотность определена функцие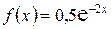й при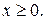

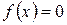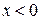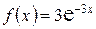4. Случайная величина Х распределена по показательному закону: при , при 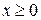. Найти вероятность попадания значений этой величины в интервал .

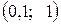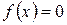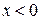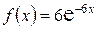5. Случайная величина Х распределена по показательному закону: при , при 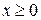. Найти математическое ожидание, дисперсию, среднее квадратическое отклонение и функцию распределения этой случайной величины. Найти вероятность попадания значений случайной величины Х в интервал .

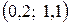6. В ящике 10 деталей, причем 7 стандартных. Какова вероятность того, что среди 6 взятых наугад деталей окажется 4 стандартных?

7. Из орудия производится стрельба по цели до первого попадания. Вероятность попадания в цель 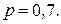Какова вероятность того, что попадание произойдет при третьем выстреле?

8. Среди 50 изделий 20 окрашенных. Найти вероятность того, что среди наугад извлеченных 5 изделий окажется ровно 3 окрашенных.

9. В партии из 12 деталей имеется 8 стандартных. Найти вероятность того, что среди 5 взятых наугад деталей окажется 3 стандартных.

ЛИТЕРАТУРА

Гмурман В. Е. Теория вероятностей и математическая статистика.– М.: Высшая школа, 2002.

Гусак А. А., Бричикова Е. А. Теория вероятностей.– Мн.: ТетраСистемс, 2000.

Лихолетов И. И., Мацкевич И. П. Руководство к решению задач по высшей математике с основами математической статистики и теории вероятностей.– Мн., 1991.

Новротская Н. Л., Петрович М. Л. Теория вероятностей. Ч. 1 и 2.– Мн.: ИУП, 1997.

Харин Ю. С., Хацкевич Г. А., Лобач В. И. Сборник задач по теории вероятностей, случайных процессов и математической статистике: Учебное пособие.– Мн.: Белгосуниверситет, 1995.

Белько И. В., Кузьмич К. К. Высшая математика для экономистов (III семестр).– М.: ООО «Новое знание», 2002.

Гмурман В. Е. Руководство к решению задач по теории вероятностей и математической статистике.– М.: Высшая школа, 1979.

Новротская Н. Л. Сборник задач по теории вероятностей: Учебное пособие.– Мн.: ЧИУП, 2005.

СОДЕРЖАНИЕ

Лекция 1. Виды случайных величин. Функции распределения вероятностей случайных величин.................................................................................. 3

1. Виды случайных величин. Закон распределения вероятностей дискретной случайной величины........................................................................................................................... 3

2. Функция распределения вероятностей случайной величины................. 10

3. Плотность распределения вероятностей непрерывной случайной величины........................................................................................................................................ 16

Лекция 2. Числовые характеристики случайной величины. Законы распределения случайных величин................................................................. 22

1. Математическое ожидание случайной величины, мода, медиана......... 22

2. Дисперсия случайной величины. Среднее квадратическое отклонение 28

3. Моменты случайных величин......................................................................... 34

4. Некоторые законы распределения случайных величин........................... 38

4.1. Формула Бернулли..................................................................................... 38

4.2. Биномиальное распределение.................................................................. 41

4.3. Распределение Пуассона........................................................................... 43

4.4. Равномерное распределение.................................................................... 45

4.5. Нормальное распределение...................................................................... 47

4.6. Некоторые другие распределения........................................................... 51

Литература............................................................................................................... 55

à

Учебное издание