
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Показательным (экспоненциальным) называют распределение вероятностей непрерывной случайной величины Х, которое описывается плотностью вероятностей
|
|
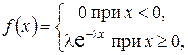
где 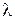 – постоянная положительная величина.
– постоянная положительная величина.
Показательный закон распределения вероятностей встречается во многих задачах, связанных с простейшим потоком событий. Под потоком событий понимают последовательность событий, наступающих одно за другим в случайные моменты. Например, поток вызовов на телефонной станции, поток заявок в системе массового обслуживания и др.
Функция распределения показательного закона имеет вид
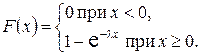

Вероятность попадания в интервал 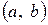 непрерывной случайной величины Х, которая распределена по показательному закону, равна
непрерывной случайной величины Х, которая распределена по показательному закону, равна
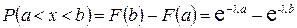 .
.
Нетрудно вычислить числовые характеристики показательного распределения:
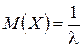 ,
, 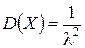 ,
, 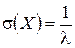 .
.
Пример 4.6.1. Непрерывная величина Х распределена по показательному закону: 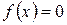 при
при 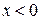 ,
, 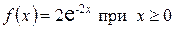 . Найти вероятность попадания значений величины Х в интервал
. Найти вероятность попадания значений величины Х в интервал 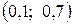 .
.
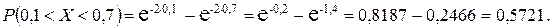
Пример 4.6.2. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х, плотность распределения которой задана функцией 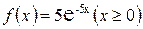 .
.
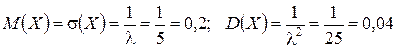 .
.
Дискретная случайная величина Х имеет геометрическое распределение, если она принимает значения 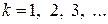 (счетное множество значений) с вероятностями
(счетное множество значений) с вероятностями
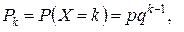
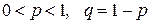 .
.
Определение является корректным, так как сумма вероятностей
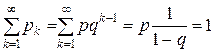 .
.
Случайная величина Х, имеющая геометрическое распределение, представляет собой число испытаний Бернулли до первого успеха.
Математическое ожидание и дисперсия Х:
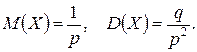
Пример 4.6.3. В большой партии изделий вероятность брака равна р. Контроль качества проводится до первого появления бракованного изделия. Обнаружилось, что бракованное изделие впервые появилось в среднем при десятом испытании. Оценить вероятность р.
Пусть Х – число испытаний до первого появления бракованного изделия. Эта случайная величина имеет геометрическое распределение. По условию ее среднее значение равно 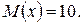 Так как
Так как 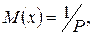 то
то 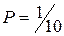 .
.
Дискретная случайная величина имеет гипергеометрическое распределение, если она принимает значения т с вероятностями
 ,
,
где 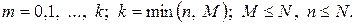
Вероятность 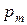 является вероятностью выбора m объектов, обладающих заданным свойством, из множества п объектов, случайно извлеченных (без возврата) из совокупности N объектов, среди которых М объектов обладают заданным свойством.
является вероятностью выбора m объектов, обладающих заданным свойством, из множества п объектов, случайно извлеченных (без возврата) из совокупности N объектов, среди которых М объектов обладают заданным свойством.
Математическое ожидание и дисперсия случайной величины, имеющей гипергеометрическое распределение с параметрами п, М, N:
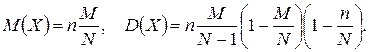
Пример 4.6.4. Среди продукции цеха электронных плат 10 из партии в 100 штук не удовлетворяют стандарту. При приемке продукции проверяются 10 плат. Какое среднее количество нестандартных плат обнаружат?
Количество нестандартных плат имеет гипергеометрическое распределение, так как
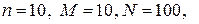 то
то 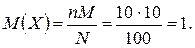
Вопросы для самопроверки
1. Как определяется показательное распределение случайной величины?
2. Какой вид имеет функция распределения для показательного закона?
3. Каково соотношение между математическим ожиданием и средним квадратическим отклонением случайной величины, имеющей показательное распределение?
4. Чему равна дисперсия случайной величины, имеющей показательное распределение?
5. Как найти вероятность попадания в заданный интервал (a, b) значений случайной величины Х, имеющей показательное распределение?
6. Какое распределение дискретной случайной величины называется геометрическим?
7. Чему равны математическое ожидание, дисперсия, среднее квадратическое отклонение геометрически распределенной случайной величины?
8. Как определяется гипергеометрическое распределение случайной величины?
9. Чему равны математическое ожидание и дисперсия случайной величины, имеющей гипергеометрическое распределение?