
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Нормальным распределением, или распределением Гаусса, называется распределение с плотностью вероятностей
|
|
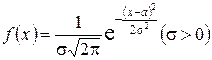 . (*)
. (*)
Постоянные а и 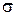 называются параметрами распределения.
называются параметрами распределения.
О случайной величине Х, плотность распределения которой определяется функцией (*), говорят, что она распределена нормально с параметрами а и 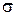 и кратко называют ее нормальной. График функции (*) называют нормальной кривой. На рис. 4.1 изображена нормальная кривая при
и кратко называют ее нормальной. График функции (*) называют нормальной кривой. На рис. 4.1 изображена нормальная кривая при 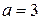 и
и 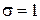 .
.
Вероятность попадания значений нормальной случайной величины Х в интервал 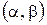 определяется формулой
определяется формулой
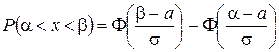 ,
,
где 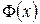 – функция Лапласа:
– функция Лапласа:
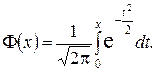
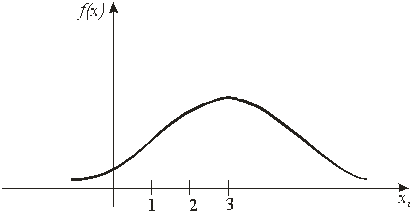
Рис. 4.1
С помощью функции Лапласа определяется и вероятность отклонения нормальной случайной величины, или вероятность неравенства 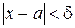 , где
, где 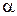 – математическое ожидание нормально распределенной величины Х:
– математическое ожидание нормально распределенной величины Х:
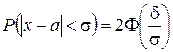 ,
,
или 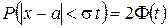 ,
,
где 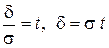 .
.
Если 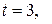 т. е.
т. е. 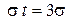 ,
,
то 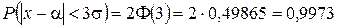 ,
,
или
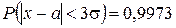 . (**)
. (**)
(Значение 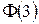 найдено с помощью таблицы значений функции Лапласа).
найдено с помощью таблицы значений функции Лапласа).
Последнее равенство означает, что событие, состоящее в осуществлении неравенства 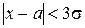 , имеет вероятность, близкую к единице, т. е. является почти достоверным.
, имеет вероятность, близкую к единице, т. е. является почти достоверным.
Формула (**) выражает правило «трех сигм»: если случайная величина распределена по нормальному закону, то модуль ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения.
В случае 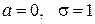 функция (*) имеет вид
функция (*) имеет вид
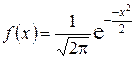 .
.
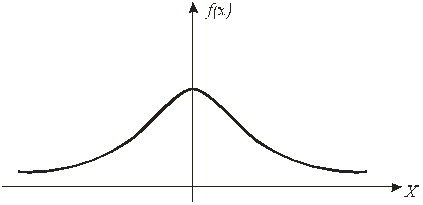
Рис. 4.2
Распределение вероятностей непрерывной случайной величины, определяемое этой функцией, называется нормированным, или стандартным. График функции f (x) называется нормированной кривой. На рис. 4.2 изображена нормированная кривая. Математическое ожидание непрерывной случайной величины Х, распределенной по нормальному закону, равно параметру а, дисперсия равна квадрату параметра 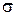 , т. е.
, т. е.
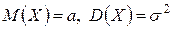 .
.
Значит, параметр 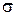 является средним квадратическим отклонением нормальной случайной величины.
является средним квадратическим отклонением нормальной случайной величины.
Пример 4.5.1. Вес пойманной рыбы подчиняется нормальному закону распределения с параметрами 
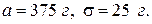 Найти вероятность того, что вес одной рыбы будет от 300 до 425 г.
Найти вероятность того, что вес одной рыбы будет от 300 до 425 г.
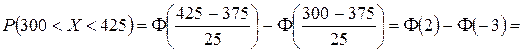
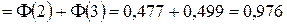 .
.
Пример 4.5.2. При измерении детали получаются случайные ошибки, подчиненные нормальному закону с параметром 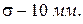 Найти вероятность того, что измерение произведено с ошибкой, не превосходящей 15 мм.
Найти вероятность того, что измерение произведено с ошибкой, не превосходящей 15 мм.
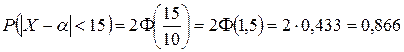 .
.
Вопросы для самопроверки
1. Какое распределение вероятностей случайной величины называют нормальным?
2. Каков вероятностный смысл параметров а и 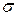 , входящих в функцию плотности вероятности?
, входящих в функцию плотности вероятности?
3. Что называют нормальной величиной?
4. Что называют нормальной кривой?
5. Чему равно математическое ожидание нормальной случайной величины?
6. Чему равна дисперсия нормальной случайной величины?
7. Чему равно среднее квадратическое отклонение нормальной случайной величины?
8. Как определяется функция Лапласа?
9. Как вычислить вероятность попадания значений нормальной случайной величины Х в заданный интервал?
10. Как вычислить вероятность отклонения нормальной случайной величины от ее математического ожидания?
11. Сформулируйте правило трех сигм.
12. Что называют стандартным отклонением?
13. Что называют нормированной кривой?
14. Какой вид имеет нормированная кривая?