
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Основные типы алгебраических структур
|
|
Алгебраические операции.
1°.Алгебраические операции.
Алгебра − наука об алгебраических операциях.
Пусть X − произвольное множество.
Определение 1. n-арной алгебраической операцией на X называется отображение 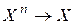 . Т.е.
. Т.е. 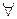 n-компонентному элементу
n-компонентному элементу  однозначно ставится в соответствие элемент
однозначно ставится в соответствие элемент 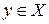 .
.
Задача. Пусть 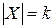 . Сколько
. Сколько 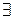 n -арных алгебраических операций на
n -арных алгебраических операций на  ? Ответ. Таких операций
? Ответ. Таких операций 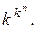
Алгебраические операции при n=1 называются унарными, при n=2 – бинарными, n=3 – тернарными. Далее, как правило, будут рассматриваться бинарные операции.
Если 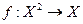 , то пишут
, то пишут 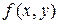 или
или 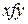 . Операции на X обозначают символами
. Операции на X обозначают символами 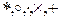 . Последний символ используется для операции сложения, остальные − для операции умножения.
. Последний символ используется для операции сложения, остальные − для операции умножения.
Определение 2. Множество X с конкретной алгебраической операцией называется алгебраической структурой.
На одном и том же множестве X могут быть заданы различные алгебраические структуры.
Примеры (алгебраических операций и алгебраических структур).
1. 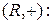 так, что
так, что 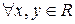 имеем
имеем 
2. 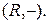 3.
3. 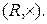
4. Деление не является алгебраической операцией на R, так как не определено деление на нуль. Однако оно является алгебраической операцией на 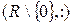 .
.
5-8. То же самое для С.
9. 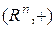
10. Скалярное произведение не является алгебраической операцией на множестве векторов, т.к.  .
.
11. 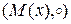 - множество всех отображений
- множество всех отображений 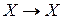 относительно операции композиции
относительно операции композиции 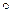 является алгебраической структурой.
является алгебраической структурой.
12. Как правило, алгебраическая операция на конечном множестве может быть задана с помощью таблицы Кэли, которая описывает результат операции на любой паре элементов множества. Рассмотрим множество, состоящее из 3-х элементов: {Доска, Окно, Тряпка} (кратко {Д, О, Т}). Введем следующую операцию, обозначаемую  (символ операции). Соответствующую таблицу Кэли можно выбрать в виде
(символ операции). Соответствующую таблицу Кэли можно выбрать в виде
 2 2
| Д | О | Т |
| Д | Д | О | Д |
| О | О | Д | Т |
| Т | Т | Т | Д |
13. Примерами тернарных операций на 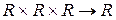 являются:
являются:
1) 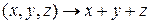 .
.
2) 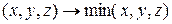 .
.
3) 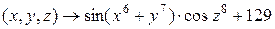 .
.
Обычно полезно изучать операции со специальными свойствами.
Определение 3. Бинарная операция 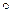 на X называется коммутативной, если
на X называется коммутативной, если 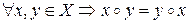 ; ассоциативной, если
; ассоциативной, если 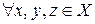 выполняется
выполняется 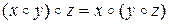 .
.
Задача. Пусть 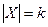 . Сколько
. Сколько 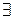 коммутативных бинарных операций на X? Ответ. Таких операций
коммутативных бинарных операций на X? Ответ. Таких операций 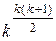 .
.