Свойства кольца.

1) Умножение дистрибутивно относительно вычитания, т.е.

.

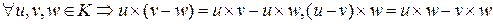Доказательство.

.

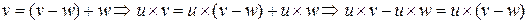2) .

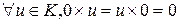Доказательство. Т.к. 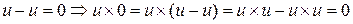. Аналогично доказывается, что .

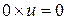Утверждение, обратное свойству 2), неверно. А именно, существуют кольца, в которых произведение двух ненулевых элементов равно нулю, т.е 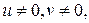но 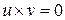. Такие кольца называются кольцами с делителями нуля. Например, множество 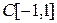непрерывных функций – кольцо с делителями нуля. Действительно, если ,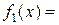

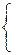
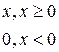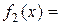
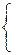
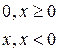
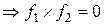
Аналогично, 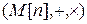− множество матриц размера 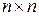− кольцо с делителями нуля.

3) Если 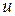− отличный от нуля элемент из 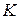, не являющийся делителем нуля, и

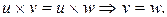(закон сокращения в кольце). Аналогично,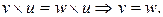

Доказательство.

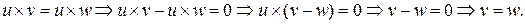
4)

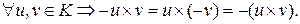
Доказательство.

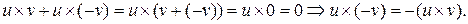
4°.Поле, свойства поля.

Пусть P – множество, содержащие не менее двух элементов.

Определение 10. Множество 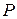с заданными на нём алгебраическими операциями сложения + и умножения 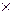называется полем и обозначается (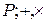), если:

1) (P; +) – абелева группа.

2) (P\{0}; 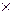) – абелева группа.

3) Умножение дистрибутивно относительно сложения, т.е.

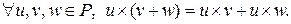
Т.о., поле – это коммутативное и ассоциативное кольцо с единицей, в котором все ненулевые элементы составляют мультипликативную группу.