Свойства группы.

1°. В группе G 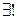нейтральный элемент и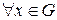 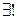симметричный элемент.

Доказательство следует из теорем 1 и 2.

2°. Для 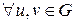уравнения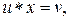 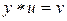имеют единственное решение:

, .

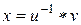Доказательство. Покажем, что 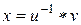– решение уравнения 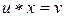. Имеем: 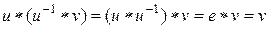, т.е. 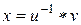− решение.

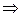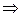
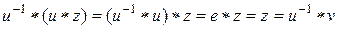
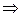
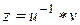
Если z – другое решение, то после умножения слева на 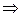x – единственное решение. Аналогично для другого уравнения.

3°. Закон сокращения в группе. Если .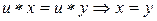

Доказательство следует из свойства 2°.

Важный пример (группа перестановок степени ).

Пусть ­­− произвольное множество из 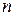элементов; например,

Определение 8. Перестановкой степени 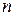называетсявзаимнооднозначное отображение множества 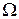в .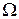

Множество всех перестановок степени 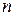обозначается 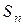. Каждую перестановку будем в дальнейшем обозначать строчной буквой греческого алфавита: 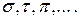Перестановка изображается двурядным символом:

.

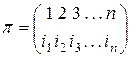Такой символ обозначает отображение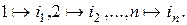

Лемма 1. Число различных перестановок степени 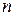равно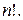

Доказательство. В качестве первого элемента 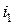можно выбрать любой из 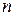элементов, в качестве второго − любой из оставшихся 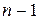элементов, и т.д. Всего различных возможностей выбора 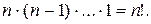Таким образом, ■

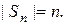На множестве перестановок вводится операция умножения по формуле

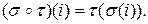Например, если

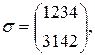
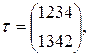то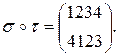

Лемма 2. Множество 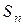образует группу, не являющуюся коммутативной.

Доказательство. Вначале проверим ассоциативность умножения. Пусть и 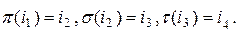Тогда по определению легко проверить выполнение равенства Тождественная перестановка является нейтральным элементом в рассматриваемом множестве, симметричный элемент получается перестановкой строк. Некоммутативность легко проверяется на предыдущем примере.■

Замечание. Если 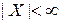и − коммутативная операция, то таблица Кэли симметрична относительно диагонали.

3°.Кольцо, свойства кольца.

В алгебре изучаются множества и с несколькими, например, с двумя, алгебраическими операциями.

Определение 9. Непустое множество 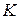называется кольцом и обозначается 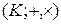, если выполняются условия:

1) (K; +) – абелева группа.

2) умножение ассоциативно, т.е.

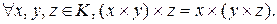
3) умножение дистрибутивно относительно сложения, т.е.

, .

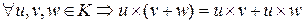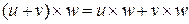Кольцо называется коммутативным (понятия абелева кольца нет!!!), если умножение коммутативно. Если относительно умножения существует нейтральный элемент, то кольцо называется кольцом с единицей.