
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Свойства поля.
|
|
1) В поле Р нет делителей нуля.
Доказательство. Пусть  Умножим
Умножим 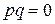 на
на 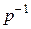 :
: 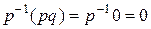 . С другой стороны,
. С другой стороны, 
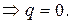
2) Свойство сокращения на ненулевой элемент: 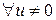 из
из 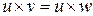
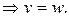
3)  , уравнение
, уравнение 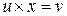 в поле P имеет единственное решение
в поле P имеет единственное решение 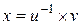 .
.
Доказательство. При 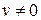 доказываемое свойство – это свойство группы, при
доказываемое свойство – это свойство группы, при 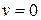 − свойство кольца.
− свойство кольца.
Решение уравнения 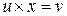 обозначается
обозначается 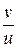 и называется частным от деления
и называется частным от деления 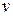 на
на 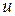 . Т.о., в поле определено деление на ненулевой элемент.
. Т.о., в поле определено деление на ненулевой элемент.
Вывод. В произвольном поле можно проводить все операции, как в обычной арифметике: сложение, вычитание, умножение, деление на ненулевой элемент, раскрытие скобок, приведение подобных, ….
Итак, алгебраические структуры – это множества с алгебраическими операциями. Дальнейшее обобщение – алгебраические системы, являющиеся совокупностью множества, алгебраических операций и отношений. Это стык алгебры и математической логики.
5°.Подполугруппа, подгруппа.
Пусть 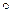 − бинарная алгебраическая операция на
− бинарная алгебраическая операция на  .
.
Определение 11. Подмножество 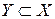 называется замкнутым относительно
называется замкнутым относительно 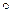 , если
, если 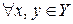 выполняется
выполняется 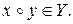
Если подмножество 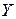 множества
множества  замкнуто относительно
замкнуто относительно 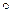 , то на
, то на 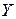 определена операция: каждой паре
определена операция: каждой паре 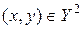 ставится в соответствие
ставится в соответствие 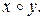
Определение 12. Такая операция на 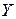 называется операцией, индуцированной операцией
называется операцией, индуцированной операцией 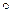 .
.
Лемма 3. Пусть 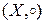 − полугруппа и
− полугруппа и 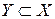 замкнуто относительно
замкнуто относительно 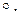 Тогда
Тогда 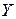 является полугруппой относительно индуцированной операции.
является полугруппой относительно индуцированной операции.
Доказательство. Длядоказательства леммы достаточно показать, что операция 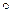 ассоциативна на множестве
ассоциативна на множестве 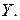 Это очевидно, так как все элементы
Это очевидно, так как все элементы 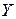 являются элементами
являются элементами  , а на
, а на  введенная операция ассоциативна.■
введенная операция ассоциативна.■
Определение 13. Пусть 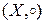 − полугруппа. Подмножество
− полугруппа. Подмножество  , замкнутое относительно
, замкнутое относительно 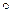 , называется подполугруппой.
, называется подполугруппой.
Пример. 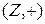 − полугруппа (и даже группа), а
− полугруппа (и даже группа), а 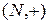 − подполугруппа (но не группа).
− подполугруппа (но не группа).
Определение 14. Пусть пара (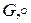 ) – группа.
) – группа. 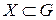 называется подгруппой, если X замкнуто относительно
называется подгруппой, если X замкнуто относительно 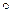 и X − группа относительно индуцированной операции.
и X − группа относительно индуцированной операции.
Определение 15. Пусть тройка (P, +, 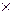 ) − кольцо (поле). Подмножество
) − кольцо (поле). Подмножество 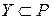 называется подкольцом (подполем), если Y замкнуто относительно
называется подкольцом (подполем), если Y замкнуто относительно  и
и 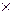 и Y является кольцом (полем).
и Y является кольцом (полем).
Пример. 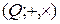 − подполе в поле
− подполе в поле 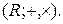
Теорема 5. Пусть (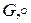 ) – группа.
) – группа. 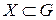 является подгруппой в
является подгруппой в 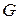

1) X замкнуто относительно 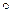 ; 2)
; 2) 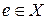 , где
, где  − нейтральный элемент в
− нейтральный элемент в 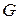 ;
;
3) 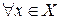 существует
существует  .
.
Доказательство. Достаточность − очевидна.
Необходимость. Пусть  − подгруппа в
− подгруппа в 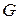 . Тогда условие 1) выполнено по определению подгруппы.
. Тогда условие 1) выполнено по определению подгруппы.
Проверим условие 2). Так как  − подгруппа, то
− подгруппа, то 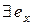 − нейтральный элемент в
− нейтральный элемент в  . Докажем, что
. Докажем, что  , т.е. совпадает с нейтральным элементом в
, т.е. совпадает с нейтральным элементом в 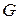 . Действительно, умножим равенство
. Действительно, умножим равенство 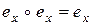 на
на 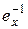 (симметричный элемент к
(симметричный элемент к 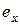 в смысле
в смысле 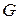 , т.е.
, т.е. 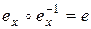 ). С одной стороны имеем:
). С одной стороны имеем:  , с другой −
, с другой − 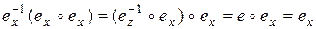 . Отсюда следует, что
. Отсюда следует, что  .
.
Осталось проверить 3). Пусть 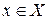 . Тогда
. Тогда 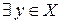 , являющийся симметричным
, являющийся симметричным 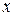 в
в  , т.е.
, т.е. 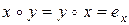 . Это и означает выполнение условия 3).■
. Это и означает выполнение условия 3).■
Аналогичные теоремы доказываются для подколец и подполей.
Теорема 6. Если в группе 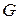 взяты две подгруппы
взяты две подгруппы  и
и 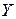 , то их пересечение
, то их пересечение 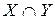 , т.е. совокупность элементов, лежащих одновременно в обоих множествах, также будет подгруппой группы
, т.е. совокупность элементов, лежащих одновременно в обоих множествах, также будет подгруппой группы 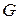 .
.
Доказательство. Действительно, если в пересечении 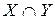 содержатся элементы
содержатся элементы 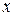 и
и 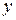 , то они лежат в подгруппе
, то они лежат в подгруппе  , а потому в
, а потому в  лежат и произведение
лежат и произведение 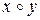 , и симметричный элемент
, и симметричный элемент 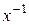 . По тем же соображениям элементы
. По тем же соображениям элементы 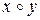 и
и 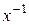 принадлежат подгруппе
принадлежат подгруппе 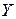 , а потому они входят и в
, а потому они входят и в 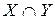 .■
.■
Интересный пример подгруппы − циклические подгруппы. Вначале введем некоторые понятия. Если  − элемент группы
− элемент группы 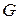 , то n- ой степенью элемента
, то n- ой степенью элемента  называется произведение n элементов, равных
называется произведение n элементов, равных  . Отрицательные степени элемента
. Отрицательные степени элемента  вводятся как произведения сомножителей, равных
вводятся как произведения сомножителей, равных 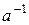 . Легко видеть, что
. Легко видеть, что 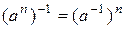 . Для доказательства достаточно взять произведение
. Для доказательства достаточно взять произведение 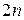 сомножителей, из которых первые
сомножителей, из которых первые 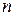 равны
равны  , а остальные −
, а остальные − 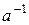 , и произвести все сокращения. Под нулевой степенью элемента будем понимать нейтральный элемент. В силу обобщенной ассоциативности легко показать, что
, и произвести все сокращения. Под нулевой степенью элемента будем понимать нейтральный элемент. В силу обобщенной ассоциативности легко показать, что 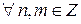 имеют место равенства:
имеют место равенства:
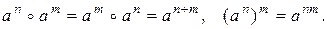
| (3) |
Обозначим 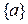 подмножество группы
подмножество группы 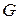 , состоящее из всех степеней элемента
, состоящее из всех степеней элемента  .
.
Лемма 4. Множество 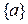 является подгруппой группы
является подгруппой группы 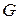 .
.
Доказательство очевидно.
Определение 16. Подгруппа 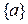 называется циклической подгруппой группы
называется циклической подгруппой группы 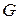 .
.
Легко видеть, что циклическая подгруппа всегда коммутативна, даже если сама группа 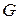 некоммутативна. Если все степени элемента
некоммутативна. Если все степени элемента  являются различными элементами, то
являются различными элементами, то  называется элементом бесконечного порядка. Если существуют
называется элементом бесконечного порядка. Если существуют 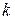 и
и 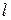 из
из 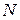 , такие, что
, такие, что  , то
, то  называется элементом конечного порядка. Легко видеть, что в этом случае
называется элементом конечного порядка. Легко видеть, что в этом случае 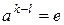 . Наименьшее
. Наименьшее 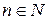 такое, что
такое, что  называется порядком элемента
называется порядком элемента  .
.
Определение 17. Группа 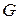 называется циклической группой, если она состоит из степеней одного из своих элементов
называется циклической группой, если она состоит из степеней одного из своих элементов  , т.е. совпадает с одной из своих циклических подгрупп
, т.е. совпадает с одной из своих циклических подгрупп 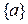 . Элемент
. Элемент  в этом случае называется образующим элементом группы
в этом случае называется образующим элементом группы 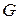 .
.