Примеры колец.

1. 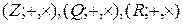образуют коммутативное кольцо с единицей относительно обычных операций сложения и умножения.

2. Множество {0}, содержащее лишь одно число 0, образует кольцо, называемое нулевым кольцом.

3. Множество 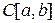непрерывных на отрезке 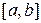функций с операциями + и , определенными следующим образом:

, ,

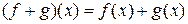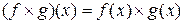образует коммутативное кольцо с единицей.

4. Множество V₃ всех векторов пространства относительно операций сложения векторов и векторного произведения векторов, образует кольцо.

5. Рассмотрим пространство битовых строк (последовательностей длины 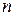, состоящих из нулей и единиц), относительно операций 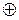(исключающее «или») и 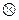(логическое умножение), которые задаются таблицами:

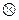
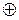
Например, (1010) 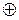(0110)=(1100); (1010) 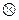(0110)=(0010).

Операци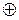и и 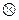− алгебраические, нейтральный элемент – нулевая битовая строка (0…0). Для каждой битовой строки противоположным элементом является эта же битовая строка. Доказательство коммутативности, ассоциативности операци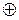й и 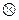и дистрибутивность логического умножения 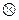относительно операции 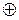сводятся к доказательству этих свойств для битовых строк длиной 1, которое проводится прямыми вычислениями. Т.о., пространство битовых строк с операциями 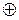, 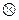является кольцом, которое обозначается 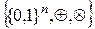. Это кольцо является ассоциативным кольцом с единицей.

Так как (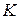; +) абелева группа, то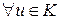 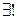противоположный элемент 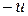. Поэтому в К можно ввести операцию вычитания: 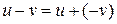.В силу свойства группы 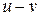единственное решение уравнения .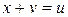