Пример. при — константах. Такое представление оказывается достаточно удобным для анализа квадратичной формы — например

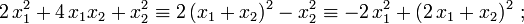
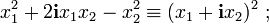
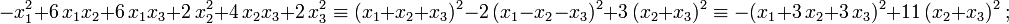
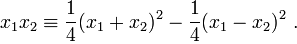
А в общем случае:

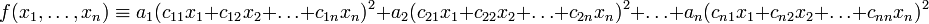
при 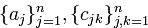— константах. Такое представление оказывается достаточно удобным для анализа квадратичной формы — например, в случае вещественных форм, при проверке выполнимости неравенства вида 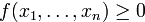. Приведенные выше примеры показывают неоднозначность представления в виде суммы квадратов: вид квадратов и даже их количество для одной и той же формы могут быть различными. С целью обеспечения некоторой унификации установим некоторое дополнительное ограничение — потребуем, чтобы линейные однородные формы

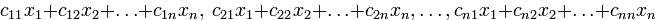
были линейно независимыми. При таком ограничении любое представление квадратичной формы в виде суммы квадратов называется каноническим видом квадратичной формы.

Задача. Для произвольной квадратичной формы 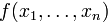построить (хотя бы один) ее канонический вид.

!

Поставленная задача имеет существенное значение для анализа

• произвольного полинома 2) нескольких переменных на максимумы и минимумы;
• геометрии линий второго порядка на плоскости и поверхностей второго порядка в пространстве; например, по набору коэффициентов уравнения, задающего кривую

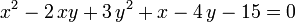
определить к какому типу (эллипс, гипербола, парабола, …) она относится.