Метод Лагранжа и метод Гаусса

§

В этом и последующих пунктах существенно потребуется знание МЕТОДА ГАУССА преобразования систем линейных уравнений.

П

Пример. Рассмотрим матрицу квадратичной формы

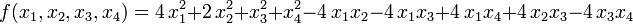
из предыдущих пунктов, и, временно выходя из круга поставленных в настоящем разделе задач, побробуем применить к ней метод Гаусса приведения к треугольному виду:

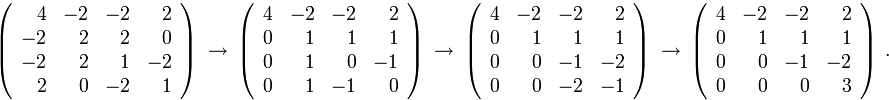
Обратим внимание на два обстоятельства: диагональные элементы последней матрицы совпадают с коэффициентами канонического вида квадратичной формы, а коэффициенты замены переменных, приводящей к этому каноническому виду, совпадают с элементами строк этой матрицы, если их разделить на соответствующие диагональные элементы. Возникает подозрение , что метод Лагранжа является «замаскированной» версией метода Гаусса. ♦

Для того, чтобы выяснить аналитический смысл преобразований по методу Лагранжа найдем правило формирования коэффициентов в первом шаге приведения квадратичной формы к каноническому виду. Пусть исходная квадратичная форма записана в виде

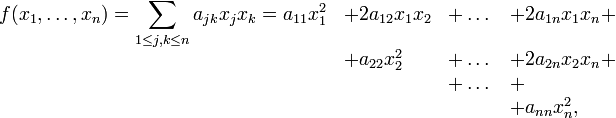
т.е. коэффициенты при смешанных произведениях переменных записаны с выделением множителя 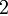. После выделения полного квадрата, содержащего переменные :

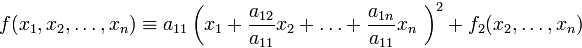
в правой части тождества образовалась квадратичная форма 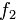, не содержащая 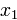. Она равна

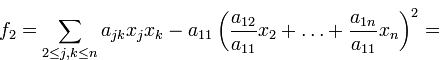
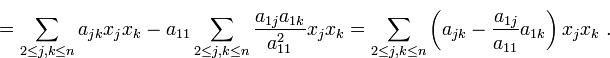
Если теперь выписать матрицу этой квадратичной формы (она имеет порядок 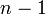), то ее элементы образуются по точно такому же правилу, как и коэффициенты матрицы, получающейся из матрицы 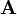в результате первого шага метода Гаусса.

Т

Теорема. Метод Лагранжа приведения квадратичной формы 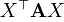к каноническому виду эквивалентен методу Гаусса приведения матрицы 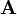к треугольному виду.

Доказательство. Действительно, первый шаг прямого хода метода исключения переменных Гаусса преобразует матрицу 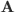следующим образом:

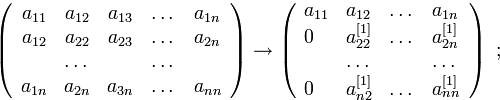
здесь

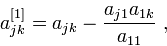
и предполагается, что 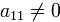. Видим, что формула формирования элементов матрицы

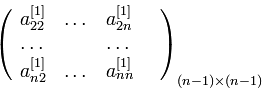
точно такая же, как и матрицы квадратичной формы 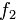. Более того, поскольку матрица 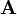симметрична (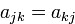), то и только что полученная матрица оказывается симметричной. Если 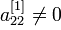, то к этой новой матрице можно снова применить ту же процедуру, и т.д., и в конце концов придем к матрице первого порядка. Собирая все промежуточные результаты в одну матрицу, получим ее в треугольном виде

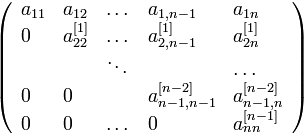
при условии, что ни одно из чисел на диагонали не обратилось в нуль:

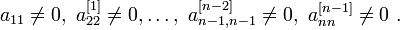
Если теперь обратиться к методу Лагранжа, то увидим, что полученная матрица как раз и определяет замену переменных

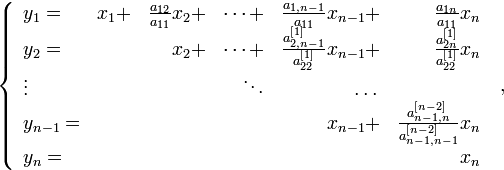
приводящую квадратичную форму к каноническому виду: