Метод Лагранжа приведения квадратичной формы к каноническому виду

Существует универсальный алгоритм, приводящий произвольную квадратичную форму к каноническому виду.

Метод Лагранжа

1. Пусть 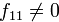. Выделим в 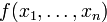все слагаемые, содержащие :

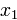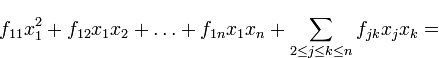
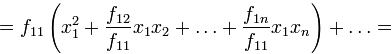
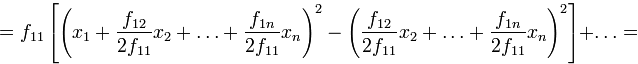
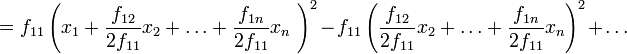
В последнем представлении первое слагаемое представляет собой квадрат линейной формы по переменным ; все оставшиеся слагаемые не зависят от 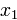, т.е. составляют квадратичную форму от переменных 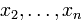. Таким образом, исходная задача для формы 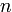переменных оказывается сведенной к случаю формы 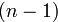-й переменной; последняя преобразуется по аналогичному принципу.

2. Если 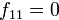, но 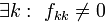, т.е. при хотя бы одном квадрате переменной коэффициент отличен от нуля. Алгоритм модифицируется таким образом, что выделение полного квадрата начинается с переменной 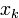вместо 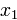— первая ничем не лучше (и не хуже) 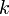-й!

3. Совсем исключительный случай: квадраты переменных вообще отсутствуют, т.е. 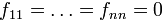. Выбираем один из ненулевых коэффициентов при смешанных произведениях переменных: пусть 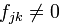. Представляем 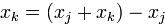и заменяем все вхождения переменной 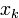на 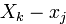при вспомогательной переменной 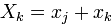. В новой квадратичной форме уже присутствует квадрат переменной 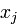с ненулевым коэффициентом. Тем самым этот случай сводится к предыдущему. После приведения новой формы к сумме квадратов возвращаемся к «старой» переменной .

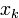П

Пример. Привести форму

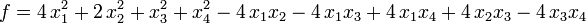
к каноническому виду.