Решение. В соответствии с алгоритмом, на следующем шаге нужно выделять слагаемые, содержащие переменную , но коэффициент при в правой части формулы обратился в нуль

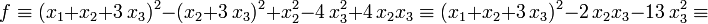
В соответствии с алгоритмом, на следующем шаге нужно выделять слагаемые, содержащие переменную 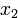, но коэффициент при 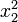в правой части формулы обратился в нуль. Поэтому — в соответствии с пунктом 2 метода — приходится выделять квадрат на основе переменной :

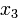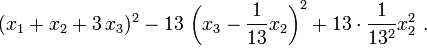
Ответ. .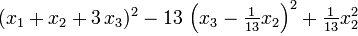

П

Пример. Привести форму

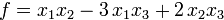
к каноническому виду.

Решение. Коэффициенты при квадратах переменных все равны нулю. Действуем в соответствии с пунктом 3 метода Лагранжа. Поскольку коэффициент при 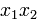отличен от нуля, делаем замену переменно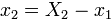й при :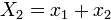

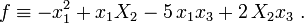
Дальнейший ход решения — в соответствии с пунктом 1 метода Лагранжа:

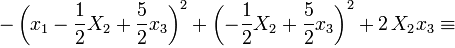
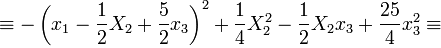
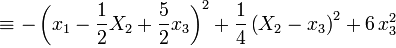
Получили сумму квадратов форм от переменных 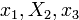. Возвращаемся к переменной :

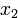Ответ. .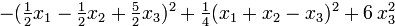

§

Метод Лагранжа позволяет получить канонический вид квадратичной формы над тем же множеством 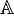, над которым рассматривается исходная форма — например, если коэффициенты формы 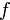являются рациональными, то и коэффициенты ее канонического вида (т.е. числа 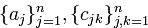) будут также рациональными.