Матричная форма записи квадратичной формы

§

В этом и последующих пунктах существенно потребуется знание ключевых понятий ТЕОРИИ МАТРИЦ и ОПРЕДЕЛИТЕЛЕЙ.

Задача. Установить правило формирования коэффициентов канонического вида квадратичной формы, получающегося применением метода Лагранжа.

Прежде всего, соберем все переменные в один вектор, а вернее — в два вектора:

столбец переменных 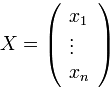и строку переменных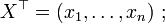

здесь 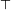означает транспонирование. Не очень принципиально, что обозначать через 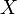— столбец или строку; и хотя сокращение 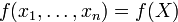кажется не вполне корректным с точки зрения только что введенного обозначения, тем не менее не будем навешивать в правую часть дополнительных значков…

Если определить верхнетреугольную матрицу 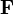равенством:

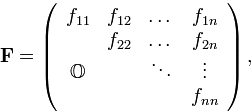
то квадратичную форму можно записать в виде произведения трех матриц

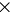строка переменных матрица столбец переменных

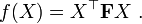
Более того, можно написать бесконечно много подобных представлений для одной и той же квадратичной формы 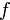, подбирая разные матрицы

П

Пример.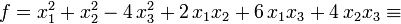

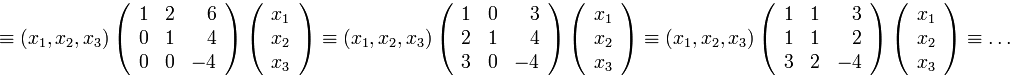
Из всего этого бесконечного множества представлений выделим одно. Рассмотрим матрицу

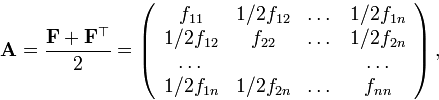
которая, очевидно, симметрична: 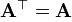. Тогда

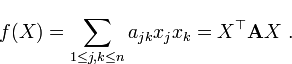
Это представление называют правильной записью квадратичной формы; матрицу 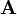называют матрицей квадратичной формы 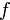, а 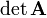— дискриминантом квадратичной формы:

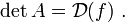
П

Пример. Для приведенной выше квадратичной формы 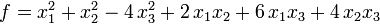ее правильной записью будет именно последняя:

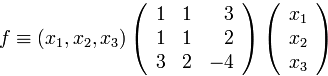
Правило формирования матрицы довольно просты: на диагонали ставятся коэффициенты при квадратах, а внедиагональные элементы получаются располовиниванием коэффициентов при смешанных произведениях переменных.

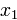
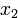
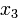
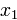
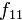
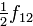
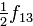
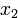
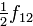
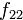
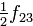
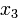
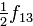
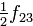
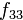
П

Пример. Для 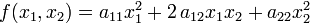имеем:

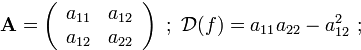
последнее выражение вполне напоминает дискриминант квадратного трехчлена 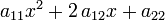и это обстоятельство оправдывает использование слова дискриминант для нового объекта…

§

Причина, по которой из бесконечного многообразия матричных представлений квадратичной формы выделяется именно то, что использует симметричную матрицу, остается пока непонятной. Отложив ненадолго обсуждение этой причины, попробуем переписать в матричных терминах приведение квадратичной формы к каноническому виду.

Рассмотрим замены переменных в квадратичной форме, т.е. переход от переменных 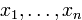к новым переменным 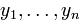. Ограничимся только линейными заменами вида

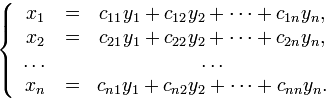
Результатом такой замены переменных будет новая квадратичная форма относительно новых переменных. Установим по какому закону формируются ее коэффициенты. С этой целью введем в рассмотрение матрицу замены переменных

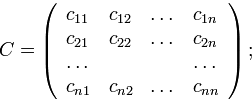
которая позволяет переписать саму замену переменных в матричном виде

Тогда формальная подстановка последнего варианта в правильную запись квадратичной формы приведет к следующей цепочке

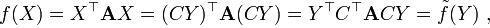
(здесь использовались некоторые свойства операции транспонирования) и, если обозначить матрицу

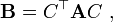
то мы получаем правило формирования матрицы квадратичной формы, получившейся в результате замены переменных, с помощью операции произведения матриц. Обратим внимание на еще один факт — матрица 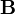является симметричной:

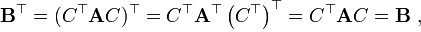
т.е. выбор в качестве матричной записи квадратичной формы именно того варианта, что основан на симметричной матрице, позволяет сохранить это свойство при любой линейной замене переменных.

Задача о нахождении канонического вида квадратичной формы 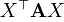может быть также переформулирована в терминах замены переменных: требуется найти такую матрицу 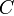, чтобы матрица 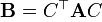оказалась диагональной:

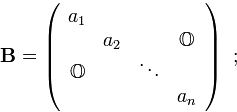
при этом дополнительным условием ставится невырожденность матрицы :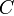

§

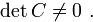
Пока не вполне понятна существенность последнего условия: почему оно накладывается? С одной стороны, оно обеспечивает обратимость замены переменных 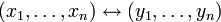— не происходит «потери информации». В самом деле, наличие какого-то ограничения на все возможные замены переменных, довольно очевидно: если бы разрешалось использовать, например, нулевую матрицу 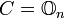, то канонический вид у любой квадратичной формы был бы нулевым… Ниже мы обсудим геометрический смысл условия .

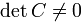Вернемся к примерам предыдущего пункта, перепишем их на матричном языке.

П

Пример. Для формы

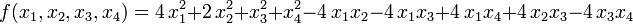
замена переменных осуществляется формулами

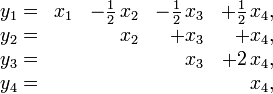
т.е. матрица замены переменных

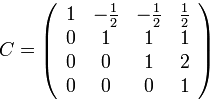
имеет верхнетреугольный вид. Канонический вид в новых переменных записывается

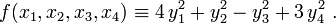
Для формы

замена переменных уже не имеет треугольного вида:

Для формы

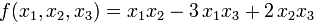
получили:

т.е. замена переменных не имеет треугольного вида. ♦

Поставленную в начале пункта задачу об установлении структуры канонического вида квадратичной формы попытаемся решить сначала для случая когда замену переменных можно подобрать именно в треугольном виде.