
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Жанама әдісі.
|
|
(3.1) тең деуді шешудің тағ ы бір классикалық ә дістерінің бірі Ньютон ә дісі. [a, b] кесіндісінде 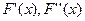 туындылары ү зіліссіз жә не белгілі таң баларын сақ тайтын болсын. Бұ л ә дістің итерациялық формуласын табу ү шін
туындылары ү зіліссіз жә не белгілі таң баларын сақ тайтын болсын. Бұ л ә дістің итерациялық формуласын табу ү шін  мұ ндағ ы
мұ ндағ ы 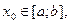 нү ктесі арқ ылы жү ргізілетін тү зу
нү ктесі арқ ылы жү ргізілетін тү зу  функциясының графигіне жанама болуы қ ажет. Ол ү шін бұ л тү зудің бұ рыштық коэффиценті
функциясының графигіне жанама болуы қ ажет. Ол ү шін бұ л тү зудің бұ рыштық коэффиценті 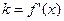 болуы керек. Жанаманың
болуы керек. Жанаманың 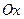 осьімен қ иылысу нү ктесінде
осьімен қ иылысу нү ктесінде  у=0 болғ андық тан
у=0 болғ андық тан
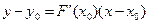
тең деуінен
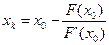 (6.1)
(6.1)
Ньютон ә дісін қ олданғ анда (3.1) тең деудің тү бірі орналасқ ан [a; b] кесіндісінің ұ штарын кө рсетудің қ ажеті жоқ, тек тү бірдің бастапқ ы жуық  мә нін беру жеткілікті.
мә нін беру жеткілікті.
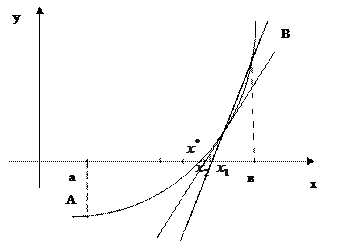
Сурет 6.1.
Бастапқ ы жуық тау ү шін [a; b] кесіндісінің бір ұ шын (Сурет –6.1-де 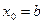 ) немесе оғ ан тиісті
) немесе оғ ан тиісті 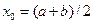 деп қ абылдауғ а болады. (6.1) формула бойынша
деп қ абылдауғ а болады. (6.1) формула бойынша 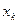 -ны табамыз, содан кейін
-ны табамыз, содан кейін 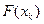 -ны есептейміз. Ә рі қ арай,
-ны есептейміз. Ә рі қ арай, 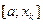 жә не
жә не 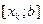 кесінділерінің қ айсысының ұ шында
кесінділерінің қ айсысының ұ шында  функциясының мә ндері ә ртү рлі таң ба қ абылдайтынын анық тап аламыз да сол аралық та, жанаманың формуласын қ айтадан қ олданамыз.
функциясының мә ндері ә ртү рлі таң ба қ абылдайтынын анық тап аламыз да сол аралық та, жанаманың формуласын қ айтадан қ олданамыз.
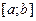 аралығ ында ү зіліссіз жә не
аралығ ында ү зіліссіз жә не 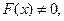
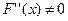 ү зіліссіз туындылары бар функция ү шін есептеу процессінің жинақ тылығ ының жеткілікті шартын анық тауғ а болады.
ү зіліссіз туындылары бар функция ү шін есептеу процессінің жинақ тылығ ының жеткілікті шартын анық тауғ а болады.
Ол ү шін 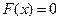 тең дігін
тең дігін 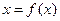 тү ріне келтірсек k-ші жуық тау бұ л жағ дайда Ньютон формуласы бойынша:
тү ріне келтірсек k-ші жуық тау бұ л жағ дайда Ньютон формуласы бойынша:

Бұ л шарт орындалуы ү шін:
1) бастапқ ы жуық тау 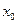 тү бірдің дә л мә ніне барынша жақ ын болады;
тү бірдің дә л мә ніне барынша жақ ын болады;
2) 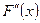 туынды аса ү лкен болмауы;
туынды аса ү лкен болмауы;
3)  туынды мү мкіншілігінше нө льден ө згеше болуы.
туынды мү мкіншілігінше нө льден ө згеше болуы.
Осы шарттар сақ талғ анда біртіндеп итерация барысында
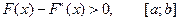 (6.2)
(6.2)
шарты орындалса, тү бірдің жуық мә ндері оның дә л мә ніне тек ғ ана бір жағ ынан жақ ындайды. Сондық тан Ньютон ә дісін қ олданғ анды бастапқ ы  жуық тау ү шін берілген кесіндінің қ ай жақ ұ шында (6.2) шарт орындалса, сол ү шін бастапқ ы жуық тау ү шін қ абылдаймыз. Жанаманың
жуық тау ү шін берілген кесіндінің қ ай жақ ұ шында (6.2) шарт орындалса, сол ү шін бастапқ ы жуық тау ү шін қ абылдаймыз. Жанаманың 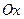 осьімен қ иылысу нү ктесі [a; b] кесіндісіне тиісті болуы ү шін жанаманы кесіндінің F(x) функциясы жә не оның екінші
осьімен қ иылысу нү ктесі [a; b] кесіндісіне тиісті болуы ү шін жанаманы кесіндінің F(x) функциясы жә не оның екінші 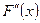 туындысының таң балары бірдей болатын ұ шында жү ргізу қ ажет. Сонда, егер
туындысының таң балары бірдей болатын ұ шында жү ргізу қ ажет. Сонда, егер 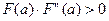 болса
болса 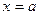 , ал
, ал  болса
болса  нү ктесінде жү ргіземіз.
нү ктесінде жү ргіземіз.