Типовые звенья САУ. Временные и частотные характеристики звеньев.

При исследовании систем управления они обычно представляются в виде взаимосвязанной совокупности отдельных элементов – динамических звеньев. Динамическим звеном называют устройство любого физического вида и конструктивного оформления, имеющее вход и выход, как показано на рисунке 2.1, и для которого задано уравнение (обычно дифференциальное), связывающее сигналы на входе и выходе.

Рисунок 2.1 – Схема динамического звена

Классификация динамических звеньев производится по виду дифференциального уравнения. Одними и теми же дифференциальными уравнениями могут описываться устройства любого типа (электрические, электромеханические, гидравлические, тепловые и т.п.), что позволяет использовать для проектирования различных устройств одинаковые подходы.

Если уравнение, связывающее сигналы , 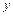линейно, то говорят о линейном динамическом звене

Уравнение линейного динамического звена имеет следующий вид:

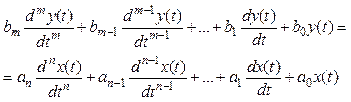(2.1)

где – постоянные коэффициенты; .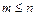

Однако вид дифференциального уравнения не является единственным признаком, по которому проводится сравнение динамических звеньев.

Основными характеристиками звеньев являются:

- дифференциальные уравнения движения;

- передаточные функции;

- временные характеристики (переходная функция, импульсная (весовая) функция;

- частотные характеристики (амплитудно-частотные характеристики, амлитудно-фазовые частотные характеристики, логарифмические частотные характеристики).

Передаточной функцией звенаназывается отношение изображений выходного и входного сигналов при нулевых начальных условиях. Подвергнем уравнение (2.1) преобразованию Лапласа, считая начальные условия нулевыми и заменяя оригиналы сигналов их изображениями:

; .

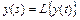Отсюда получим

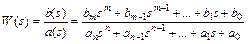(2.2)

Отношение (2.2) не зависит от изображений сигналов и определяется только параметрами самого динамического звена , , имеет вид дробно-рациональной функции.

Уравнение вида

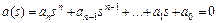(2.3)

называют характеристическим уравнением динамического звена, так как знаменатель передаточной функции – это характеристический полином дифференциального уравнения, описывающего динамическое звено.

Временные характеристики обусловливают динамические свойства звена. Они определяются на выходе звена при подаче на вход типовых сигналов.

Переходная функция или переходная характеристика 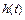представляет собой переходный процесс на выходе звена, возникающий при подаче на его вход скачкообразного воздействия при величине скачка, равного единице (рисунок 2.2). Такое воздействие называется единичной ступенчатой функцией и обозначается

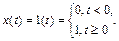(2.4)

Ступенчатая функция представляет собой распространенный вид входного воздействия в САУ. К такому виду воздействия можно отнести мгновенное изменение нагрузки электрогенератора, возрастание момента на валу двигателя, мгновенное изменение задания на частоту вращения двигателя, мгновенный поворот командной оси следящей системы.

а) б)

Рисунок 2.2 – Единичная ступенчатая (а) и переходная (б) функции

Изображение по Лапласу единичной ступенчатой функции определяется как

.

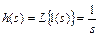Чтобы определить изображение переходной функции при известной передаточной функции звена необходимо выполнить следующую операцию:

(2.5)

Оригинал 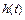находят с помощью обратного преобразования Лапласа (приложение Б), применяемого к (1.5).

импульсная переходная функция или весовая функция 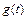– это реакция звена на единичную импульсную функцию. Единичная импульсная функция, или 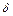– функция, представляет собой производную от единичной ступенчатой функции:

.

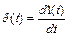Дельта-функция определяется выражением

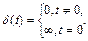(2.6)

Основное свойство дельта-функции состоит в том, что

,

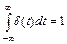то есть она имеет единичную площадь. Эту функцию можно описать как короткий, но мощный импульс. Дельта-функция также является распространенным входным воздействием в автоматических системах. Например, кратковременный удар нагрузки на валу двигателя, кратковременный ток короткого замыкания генератора, отключаемый предохранителями и т.п.

Нетрудно установить, что изображение 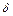-функции определяется

.

Изображение функции веса есть передаточная функция:

.

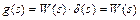Поэтому для нахождения оригинала импульсной переходной функции необходимо применить обратное преобразование Лапласа к передаточной функции звена (системы).

Дельта-функция и функция веса некоторого звена изображены на рисунке 2.3

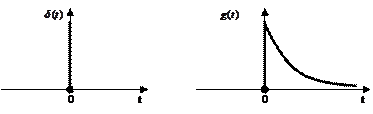
Рисунок 2.3 – Дельта функция (а) и функция веса (б)

Переходная и импульсная функции связаны соотношениями

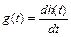; . (2.7)

Частотной характеристикой динамического звена называют функцию комплексного аргумента 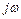, полученную путем формальной замены 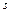на 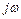в выражении передаточной функции. Частотные характеристики получают при рассмотрении движения звена (системы) при подаче на его вход гармонического воздействия.

Функцию 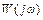, которую получают из передаточной функции (2.2):

, (2.8)

называют частотной передаточной функцией.

Частотная передаточная функция, как функция комплексного аргумента, может быть представлена в виде

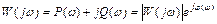, (2.9)

где 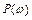– действительная (вещественная) часть 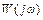; 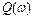– мнимая часть 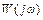; 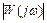– модуль (амплитуда) 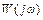; – аргумент (фаза) .

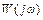Амплитуда, фаза, действительная и мнимая части функции 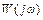являются функциями частоты, поэтому частотная передаточная функция используется и представляется в виде амплитудно-фазовой, действительной, мнимой, амплитудной и фазовой частотных характеристик.

Таким образом, в ТАУ рассматривают следующие частотные характеристики динамических звеньев:

1. Амплитудно-частотная характеристика (АЧХ) –

. (2.10)

2. Фазочастотная характеристика (ФЧХ) –

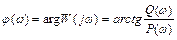. (2.11)

3. Вещественная частотная характеристика (ВЧХ) –

. (2.12)

4. Мнимая частотная характеристика (МЧХ) –

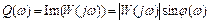. (2.13)

5. Амплитудно-фазовая частотная характеристика (АФЧХ), которая определяется как годограф вектора 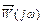(кривая, описываемая концом этого вектора), построенный на комплексной плоскости при изменении частоты 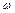от 0 до .

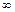Физический смысл частотных характеристик можно определить следующим образом. При гармоническом воздействии в устойчи­вых системах после окончания переходного процесса, выходная величина также изменяется по гармоническому закону, но с другими амплитудой и фазой. При этом отношение амплитуд выходной и входной величин равно модулю, а сдвиг фазы – ар­гументу частотной передаточной функции. И, следовательно, амплитудная частотная характеристика показывает изме­нение отношения амплитуд, а фазовая частотная харак­теристика – сдвиг фазы выходной величины относительно вход­ной в зависимости от частоты входного гармонического воздей­ствия.

Общий вид частотных характеристик представлен на рисунке 2.4.

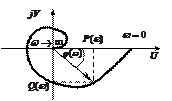
а)

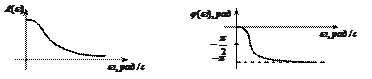
б) в)

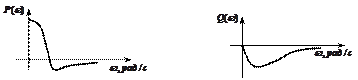
г) д)

Рисунок 2.4 – Частотные характеристики:

амплитудно-фазовая (а), амплитудно-частотная (б), фазо-частотная (в), вещественная частотная (г), мнимая частотная (д)характеристики

Логарифмические частотные характеристики (ЛЧХ). Логарифмической амплитудной частотной характеристикой (ЛАЧХ) динамического звена называют такое представление амплитудной частотной характеристики (АЧХ), в котором модуль (амплитуда) частотной характеристики выражен в децибелах, а частота – в логарифмическом масштабе:

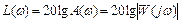. (2.14)

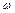Логарифмической фазовой частотной характеристикой (ЛФЧХ) динамического звена называют график зависимости фазо-частотной характеристики (ФЧХ) от логарифма частоты. При построении логарифмических характеристик по оси абсцисс откладывают частоту в логарифмическом масштабе, а на отметке, соответствующей значению , пишут само значение . Довольно часто ЛАЧХ и ЛФЧХ строятся на одном графике, чтобы давать полное представление о свойствах объекта.

Единицей 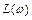является децибел, а единицей логарифма частоты в ЛЧХ – декада. Декадой называют интервал, на котором частота изменяется в 10 раз. При изменении частоты в 10 раз говорят, что она изменилась на одну декаду.

При построении ЛФЧХ отсчет углов идет по оси ординат в обычном масштабе в градусах или радианах.

Ось ординат при построении ЛЧХ проводят через произво­льную точку, а не через точку 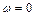(частоте 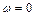соответ­ствует бесконечно удаленная точка: 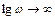при 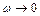). Так как 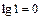, то начало координат чаще всего берется в точке .

Частота 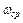, на которой 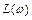пересекается с осью абсцисс, называется частотой среза. Ось абсцисс соответствует значению 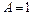, т.е. прохождению амплитуды входного сигнала через звено в натуральную величину. Верхняя полуплоскость ЛАЧХ соответствует значениям 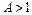(усиление амплитуды), а нижняя полуплоскость – значениям (ослабление амплитуды).

На рисунке 2.5 изображен примерный вид и оформление ЛАЧХ и ЛФЧХ некоторого инерционного звена.

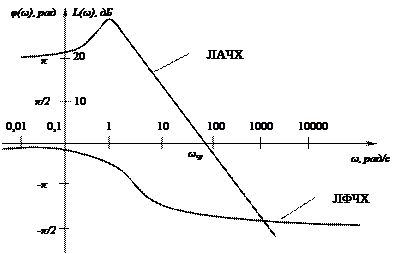
Рисунок 2.5 – Логарифмические частотные характеристики

ниже приводятся наименования некоторых типовых динамических звеньев и описывающие их уравнения:

1. Безынерционное (масштабирующее, пропорциональное) звено

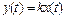. (2.15)

2. Дифференцирующее звено

. (2.16)

3. Интегрирующее звено

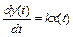. (2.17)

4. Апериодическое звено первого порядка

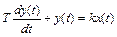. (2.18)

5. Апериодическое звено второго порядка

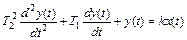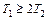, . (2.19)

6. Колебательное звено

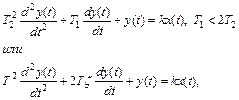(2.20)

где – параметр затухания колебаний (); – угловая частота свободных колебаний (при отсутствии затухания).

Кроме перечисленных основных к типовым часто относят следующие звенья.

7. Реальное дифференцирующее звено (дифференцирующее с замедлением)

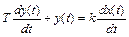. (2.21)

8. Интегрирующее звено с замедлением

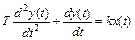. (2.22)

Здесь – коэффициент усиления звена, – постоянная времени, с.