Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Алгебраические критерии устойчивости (критерий Гурвица, Рауса).
|
|
Критерий Рауса является алгебраическим критерием определения устойчивости. Применяется для замкнутой САУ.
Согласно критерию строится таблица. На первом этапе строятся две первые строки таблицы Рауса:
| 11) | an | an-2 | a1 { a0 } |
| 22) | an-1 | an-3 | a0 { 0 } |
где an – коэффициент характеристического многочлена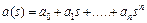 
при s n; an-2 – коэффициент при s n-2 и т.д.
Затем строится промежуточная строка, для чего вторая строка умножается на число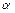 
и складывается с первой строкой:
| 
| ……… |  
|
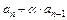
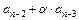
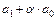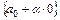
Причем 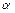выбираем так, чтобы элемент первого столбца был равен нулю 
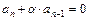.Отсюда следует, что 
(
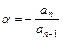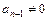, иначе не выполняется необходимый критерий устойчивости).
Таким образом, получаем строку
|
| ……… | 
|
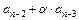
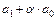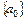
Третья строка получается из промежуточной путем циклического сдвига влево:
| 3) |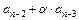
| ……… |
|
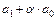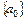
Если элемент первого столбца меньше либо равен нулю, то это означает, что система неустойчива; если больше нуля, то таблица строиться дальше: по второй и третьей строкам строится аналогично четвёртая и т.д. Построение продолжается до тех пор, пока либо в первом столбце появиться элемент меньше или равный нулю, тогда система не устойчива, либо будет построена (n+ 1)-я строка и все элементы первого столбца таблицы окажутся положительными, что является необходимым и достаточным условием устойчивости системы.
Критерий Гурвица также относится к алгебраическим критериям определения устойчивости.
Он основан на построении и анализе матрицы Гурвица 
, которая имеет размеры 
и составляется из коэффициентов характеристического многочлена замкнутой системы по правилу:
1) по главной диагонали матрицы снизу вверх выписывается последовательно n коэффициентов характеристического уравнения от а1 до аn;
2) столбцы матрицы образуются из коэффициентов характеристического уравнения, записанных вверх от главной диагонали в порядке возрастания индексов, а вниз – в порядке их убывания;
3) если индекс коэффициента становится меньше нуля или больше n, то на место такого коэффициента становится ноль.
.
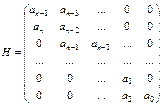Необходимое и достаточное условие устойчивости заключается в положительности всех диагональных миноров 
(при условии, что 
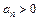). Каждый из миноров – это определитель, и вычисляется по правилам вычисления определителей. Например, 
, 
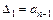и т.д.
Если характеристический полином замкнутой системы имеет второй порядок, то необходимым и достаточным условием устойчивости будет являться положительность всех коэффициентов. Если порядок полинома равен трем, то к предыдущему условию добавляется выполнение неравенства
,
которое вытекает из правила вычисления определителя второго порядка и формулировки критерия Гурвица.