Качество переходного процесса. Прямые показатели и косвенные методы оценки качества переходного процесса.

Цель работы САУ заключается в том, чтобы как можно точнее выполнялось равенство 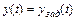, то есть выходная координата равнялась входной, и ошибка ,

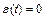где 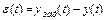(8.1)

Выполнение равенства (8.1) характеризуют показателями качества.

Близость 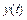и 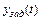при отдельных значениях t характеризуют прямыми показателями качества, которые определяются по графику переходной функции h(t) (рисунок 8.1).

Рисунок 8.1– График переходной функции САУ

К прямым показателям качества относятся.

1. Время регулирования 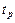– время, начиная с которого, все значения переходной функции h(t) принадлежат пятипроцентному коридору Δ от установившегося значения.

2. Перерегулирование 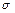– максимальное отклонение переходной функции от установившегося значения, выраженное в процентах

.

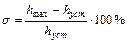Допустимое значение 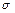обычно составляет 10–30%. Иногда перерегулирование недопустимо.

3. Частота колебаний для периодических процессов .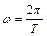

4. Число колебаний n.

5. Время достижения первого максимума t_max1.

6. Время нарастания 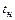– абсцисса первой точки пересечения переходной характеристики h(t) с уровнем h_уст.

7. Декремент затухания χ, равный отношению модулей двух смежных перерегулирований

.

В установившемся режиме САУ характеризуется точностью (рисунок 8.2)

Рисунок 8.2 – Графики изменения и точности выходных величин САУ

Точность обычно рассматривают при 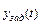, представляющих скачок по положению 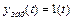, скачок по скорости и скачок по ускорению .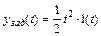

Точность определяется установившейся ошибкой , которая обычно характеризуется коэффициентами ошибок С₀, С₁, С₂,.... Коэффициенты ошибок вычисляются путем представления установившейся ошибки по производным задающего воздействия.

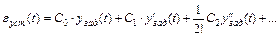(8.2)

Таким образом, C₀ характеризует влияние на установившуюся ошибку 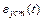величины входного сигнала, С₁ – скорости изменения входного сигнала, С₂ – ускорения входного сигнала и т.д. Коэффициенты ошибок могут быть вычислены по формулам:

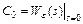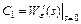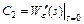; ; ; … (8.3)

Здесь – передаточная функция от входа 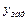до выхода 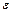, определяющаяся выражением

,

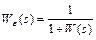где – передаточная функция разомкнутой системы.

Под частотными показателями качества САУ понимаются такие показатели, которые не предполагают знание вида переходного процесса, а базируются на некоторых частотных свойствах системы.

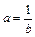На основе критерия Найквиста определяются запасы устойчивости по фазе и по амплитуде , характеризующие степень удаленности частотного годографа от точки 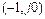, то есть степень устойчивости системы.

Для устойчивой САУ запасы устойчивости по фазе и амплитуде определяются так, как показано на рисунке 3.8.

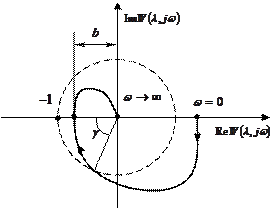
Рисунок 8.3 – Запасы устойчивости по амплитуде и фазе

Прямые показатели качества могут быть оценены по виду вещественной частотной характеристики (ВЧХ) 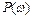. Основой этих оценок служат следующие свойства ВЧХ.

1. Установившееся значение 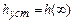переходной функции определяется начальным значением вещественной частотной характеристики: .

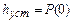2. Начальное значение переходной характеристики определяется конечным значением вещественной частотной характеристики: .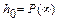

3. Двум ВЧХ, сходным по форме, но отличающимся масштабом по оси абсцисс в 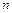раз, соответствуют переходные характеристики, также сходные по форме и отличающиеся масштабом по оси абсцисс в 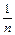раз. Если вещественной частотной характеристике соответствует переходная характеристика 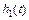(рисунок 8.4), то вещественной частотной характеристике 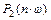соответствует переходная характеристика .

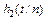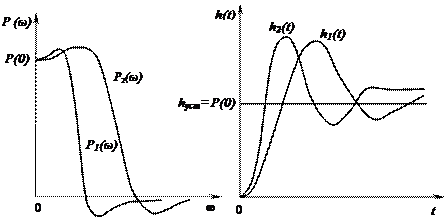
а) б)

Рисунок 8.4 – Вещественные частотные характеристики а) и соответствующие им переходные характеристики б)

4. Двум вещественным частотным характеристикам, сходным по форме, но отличающимся масштабом по оси ординат в 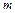раз, соответствуют переходные характеристики, также сходные по форме и отличающиеся масштабом по оси ординат в 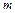раз.

5. Разрыв непрерывности ВЧХ свидетельствует о том, что система находится на границе устойчивости. Разрыву при 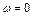соответствует апериодическая граница устойчивости (характеристическое уравнение имеет нулевой корень). Разрыву при 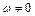соответствует колебательная граница устойчивости (характеристическое уравнение имеет пару комплексно-сопряженных корней).

6. Острый пик ВЧХ при угловой частоте 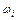, 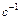свидетельствует о медленно затухающих колебаниях переходной характеристики с частотой, близкой к 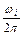, Гц.

7. Если вещественная частотная характеристика непрерывная положительная и имеет вид вогнутой кривой, то есть её производная 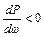, и монотонно уменьшается по абсолютному значению, то переходная характеристика монотонная.

8. Если при какой-либо частоте ордината ВЧХ больше начальной, то переходная характеристика не монотонная.

9. При положительной невозрастающей ВЧХ перерегулирование переходной характеристики не превышает 18%.

10. При наличии у положительной ВЧХ максимума 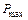перерегулирование переходной характеристики оценивают неравенством

.

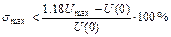11. Если ВЧХ имеет положительный 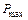и отрицательный 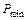экстремумы, как показано на рисунке 8.5, то перерегулирование переходной характеристики оценивают неравенством:

.

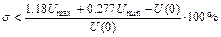Рисунок 8.5 – ВЧХ с двумя экстремумами

12. Время регулирования, в случае, если ВЧХ непрерывная невозрастающая, определяется по формуле .

13. Если ВЧХ положительная на интервале частот , то в этом случае время регулирования 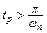.