
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Переходные процессы в САУ. Методы построения переходных характеристик систем.
|
|
Переходный процесс в теории систем представляет реакцию динамической системы на приложенное к ней внешнее воздействие с момента приложения этого воздействия до некоторого установившегося значения во временной области. Изучение переходных процессов — важный шаг в процессе анализа динамических свойств и качества рассматриваемой системы.
Переходная функция есть частный случай переходного процесса САУ. Переходная функция или переходная характеристика 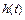 - это переходный процесс на выходе звена, возникающий при подаче на его вход скачкообразного воздействия при величине скачка, равного единице (рисунок 10.1). Такое воздействие называется единичной ступенчатой функцией и обозначается
- это переходный процесс на выходе звена, возникающий при подаче на его вход скачкообразного воздействия при величине скачка, равного единице (рисунок 10.1). Такое воздействие называется единичной ступенчатой функцией и обозначается

Ступенчатая функция представляет собой распространенный вид входного воздействия в САУ. К такому виду воздействия можно отнести мгновенное изменение нагрузки электрогенератора, возрастание момента на валу двигателя, мгновенное изменение задания на частоту вращения двигателя, мгновенный поворот командной оси следящей системы.


а) б)
Рисунок 10.1 – Единичная ступенчатая (а) и переходная (б) функции
Для решения задачи построения переходной функции используются:
– преобразование Лапласа (прямое и обратное);
– численные методы.
Изображение единичной ступенчатой функции определяется как
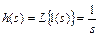 .
.
Чтобы определить изображение переходной функции при известной передаточной функции звена  необходимо выполнить следующую операцию:
необходимо выполнить следующую операцию:
 (10.2)
(10.2)
Оригинал 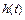 находят с помощью обратного преобразования Лапласа, применяемого к (10.2).
находят с помощью обратного преобразования Лапласа, применяемого к (10.2).
В теории автоматического управления обычно используются дробно–рациональные функции-изображения (например, передаточные функции системы).
Если функция  дробно-рациональная, причем степень многочлена-числителя меньше степени многочлена-знаменателя, то оригиналом служит функция
дробно-рациональная, причем степень многочлена-числителя меньше степени многочлена-знаменателя, то оригиналом служит функция
 , (10.3)
, (10.3)
где 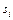 – полюсы
– полюсы 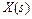 (корни
(корни  ),
), 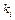 – их кратности и сумма берется по всем полюсам.
– их кратности и сумма берется по всем полюсам.
В частности, если отсутствуют кратные полюсы, то формула (10.3) имеет вид
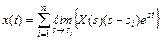 . (10.4)
. (10.4)
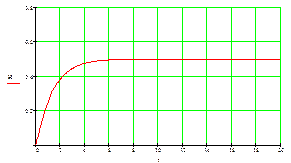
Рисунок 10.2 – Типовой график переходного процесса