Частотные критерии устойчивости (Михайлова, Найквиста)

Частотный критерий Михайлова позволяет судить об устойчивости по виду частотного годографа 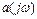характеристического многочлена замкнутой системы.

Частотным годографом характеристического многочлена

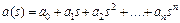
называется кривая, которую описывает конец радиус-вектора 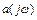при .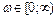

В основе критерия Михайлова лежит принцип аргумента, заключающийся в том, что изменение (приращение) аргумента вектора 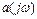при изменении частоты 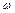от до 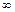равно разности между числом левых и правых корней характеристического уравнения системы, умноженной на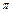

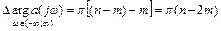, (6.1)

где 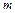– число корней характеристического многочлена в правой полуплоскости; n – степень характеристического многочлена (количество всех корней).

Очевидно, что при 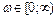приращение аргумента будет в два раза меньше

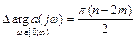. (6.2)

Из (6.2) следует расчетная формула критерия Михайлова

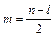, (6.3)

где l – приращение аргумента частотного годографа многочлена, выраженное в числе квадрантов (четвертей комплексной плоскости).

Если система устойчива, то есть все корни характеристического многочлена лежат слева от мнимой оси, и m =0. Тогда формула (6.3) примет вид:

.

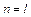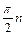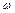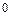Отсюда следует, что САУ устойчива, если приращение аргумента частотного годографа характеристического многочлена замкнутой системы равно , причем годограф не должен проходит через начало координат. Критерий формулируется следующим образом: для того, чтобы САУ была устойчива, необходимо и достаточно, чтобы годограф Михайлова при изменении частоты от до 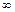, начинаясь при 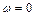на вещественной положительной полуоси, обходил только против часовой стрелки последовательно 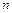квадрантов координатной плоскости.

Частотный критерий Найквиста позволяет судить об устойчивости замкнутой системы по виду амплитудо-фазовой характеристики разомкнутой системы (частотного годографа передаточной функции ).

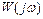Частотным годографом передаточной функции называется кривая, которую описывает конец радиус-вектора при .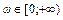

Критерий также основан на принципе аргумента. Расчетная формула критерия Найквиста имеет вид:

,

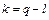где – число правых корней характеристического многочлена замкнутой системы; 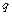– число правых корней характеристического многочлена разомкнутой системы; 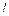– приращение аргумента частотного годографа многочлена, выраженное в числе квадрантов.

Для устойчивой замкнутой системы 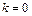и тогда . Если и разомкнутая не имеет полюсов справа от мнимой оси, то , что влечет 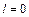. Таким образом, если разомкнутая система устойчива, то замкнутая система будет устойчивой тогда и только тогда, если приращение аргумента частотного годографа разомкнутой системы относительно точки 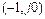равно нулю. Для систем с нулевым порядком астатизма это соответствует тому, что частотный годограф разомкнутой системы не должен охватывать точку 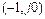, как показано на рисунке 6.1, а.

а)

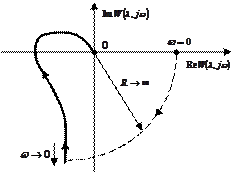
б)

Рисунок 6.1 – Частотные годографы Найквиста статической а)

и астатической б) систем

Если разомкнутая система неустойчива, то замкнутая система будет устойчива тогда, и только тогда, когда годограф разомкнутой системы охватывает точку 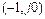в положительном направлении (против часовой стрелки) раз при .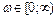

Если система астатическая и в случае разрывного годографа, его график достраивается дугами окружностей бесконечно большого радиуса до непрерывного, начиная с вещественной оси, по часовой стрелке.

В случае астатической системы первого порядка дуга достраиваемой окружности имеет численное значение 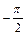(рисунок 6.1, б). Затем применяется критерий Найквиста к полученной непрерывной кривой.