Случайные величины

Для моделирования различных физических, экономических и прочих процессов часто бывает необходимым иметь случайные процессы и случайные величины с известными законами распределения. В среде Mathcad существует ряд встроенных функций, которые позволяют получать последовательность значений случайной величины по известному распределению. Таким образом, существует генератор случайных чисел, создающий выборку псевдослучайных данных с соответствующим законом распределения.

Пример (рис.17).

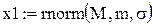
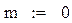
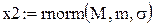
Рис.17

Перечислим встроенные функции, которые рассчитывают числовые характеристики этого распределения:

- dnorm(x, m, σ) – плотность вероятности нормального распределения (рис.18);

- pnorm(x, m, σ) – функция нормального распределения (рис.19);

- cnorm(x) – фунция нормального распределения с нулевым математическим ожиданием и единичной дисперсией;

- qnorm(F, m, σ) – обратная функция нормального распределения;

- rnorm(M, m, σ) – вектор М независимых случайных чисел, каждое из которых имеет нормальное распределение.

x – значение случайной величины; Р – значение вероятности; m – математическое ожидание; σ – среднеквадратичное отклонение.

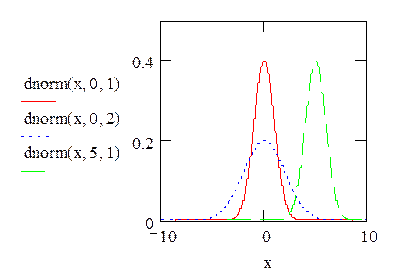
Рис.18

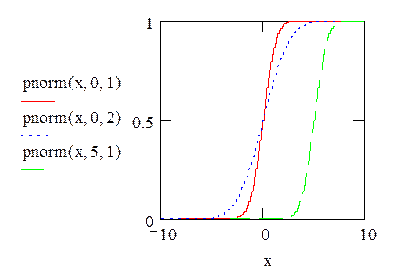
Рис.19

Функция распределения вероятностей F(x) – это вероятность того, что случайная величина примет значение меньшее или равное х. Функция, обратная F(x), называемая квантилем распределения, позволяет по заданному аргументу р определить значение х так, что случайная величина будет меньше или равна х с вероятностью р.

Приведем несколько примеров использования рассматриваемых функций.

Пример 1. Вероятность того, что случайная величина примет значение меньше 1.5.

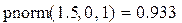
Пример 2. Нахождение 95%-ного квантиля нормального распределения.

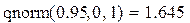
Пример 3. Вероятность того, что значение случайной величины будет больше 1.

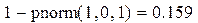
Пример 4. Вероятность того, что значение случайной величины находится в интервале (2, 3).

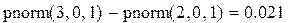
Пример 5. Вероятность того, что -2< x< 2.

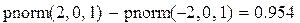
Пример 6. Вероятность того, что значение случайной величины находится в интервале (2, 3) для случая нормального распределения с ненулевым математическим ожиданием и произвольной дисперсией.

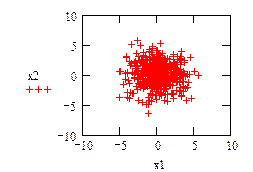
Пример 7. Генерация двух векторов с нормальным законом распределения (m -математическое ожидание, σ - среднеквадратичное отклонение распределения). Размерность векторов равна 500. На рис.20 изображено распределение полученных точек на плоскости.

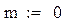
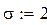
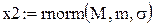
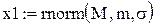
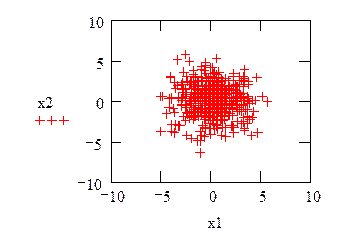
Рис.20