Полиномиальная сплайн-интерполяция

Интерполяция полиномом – это интерполяция заданной на интервале функции полиномом, степень которого определяется количеством узлов на данном интервале. Однако в среде Mathcad полиномиальная сплайн-интерполяция подразумевает кусочную интерполяцию или интерполяцию сплайнами, но уже не кубическими. Сплайнами могут быть полиномы первой, второй или третьей степени. Такие сплайны называются В-сплайнами. Применяется интерполяция В-сплайнами точно так же, как обычная сплайн-интерполяция, различие состоит только в определении вспомогательной функции коэффициентов сплайна.

Опишем встроенные функции для этого типа интерполяции:

- interp(s, x, y, t) – функция, интерполирующая данные векторов x, y с помощью В - сплайнов;

- bspline(x, y, u, n) – вектор значений коэффициентов В-сплайна;

- s – вектор вторых производных, созданный функцией bcpline;

-x – узлы интерпорляции, расположенные в порядке возрастания;

-y – значения функции в узлах;

-t – значение аргумента, при котором вычисляется интерполирующая функция;

- u – вектор значений аргумента, в которых производится сшивка В-сплайнов;

- n – порядок полиномов в данной сплайн-интерполяции.

Замечание. Размерность вектора u должна быть на 1, 2 или 3 меньше размерности векторов x и y. Первый элемент вектора u должен быть меньше или равен первому элементу вектора х, а последний элемент вектора u – больше или равен последнему элементу вектора х.

Интерполяция В-сплайнами иллюстрируется следующим примером.

Пример (рис.28).

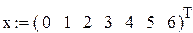
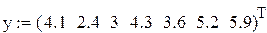
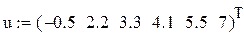
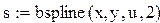
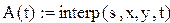
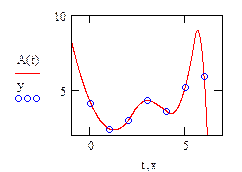
Рис.28