Сплайн-интерполяция

В большинстве задач точки удобно соединять не ломаной, а кривой. Для этой цели наиболее подходящей является кривая, которая представляет собой совокупность отрезков кубических кривых (или кубических сплайнов), гладко сшитых в узловых точках. Опишем основные встроенные процедуры, которые позволяют использовать кубическую сплайн-интерполяцию:

- interp(s, x, y, t) – функция, интерполирующая данные векторов x, y кубическими сплайнами;

- s – вектор вторых производных, созданный из одной из сопутствующих функций точках csline, pspline, lspline и необходимый для гладкого сшивания сплайнов в узловых точках;

- x – узлы интерполяции;

- y – значения функции в узлах;

- t – значение аргумента, при котором вычисляется интерполирующая функция;

- lspline(x, y) – вектор значений коэффициентов линейного сплайна;

- pspline(x, y) – вектор значений коэффициентов квадратичного сплайна;

- csline(x, y) – вектор значений коэффициентов кубического сплайна.

Пример (рис.27).

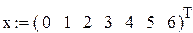
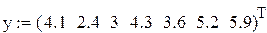
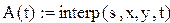
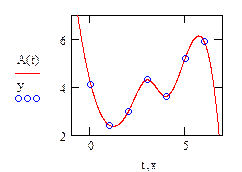
Рис.27