Распределение Пуассона. Определение. СВДТ Х имеет распределение Пуассона с параметром , если ее возможные значения (реализации)

Определение. СВДТ Х имеет распределение Пуассона с параметром 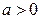, если ее возможные значения (реализации) 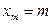, где 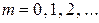(счетное множество значений), а соответствующие им вероятности выражаются формулой:

.

Замечание. Это распределение зависит от одного параметра a, поэтому пишут .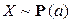

Важнейшие числовые характеристики :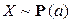

, , .

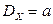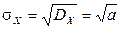Вывод. Параметр a в распределении Пуассона является одновременно математическим ожиданием и дисперсией.

Теорема (Пуассон). Если и 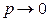так, что 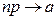, то для любого фиксированного значения m ()

.

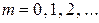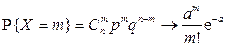Комментарий. Из теоремы Пуассона следует, что распределение Пуассона является предельным для биноминального распределения, когда число опытов n неограниченно увеличивается () и одновременно параметр p (вероятность «успеха» в одном опыте) неограниченно уменьшается (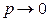), но так, что их произведение 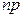сохраняется в пределе постоянным и равным a, т.е. 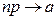(на практике 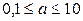). Значит, распределение Пуассона с параметром 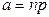можно применять для приближенных вычислений вместо биномиального, когда число опытов n очень велико, а вероятность p «успеха» в отдельном опыте очень мала, т.е. в каждом отдельном опыте «успех» приходит редко. Поэтому закон Пуассона в литературе часто называется «законом редких явлений».

Пример 2.1.28. Завод отправил на базу 5000 доброкачественных изделий. Вероятность того, что в пути изделие повредится, равна 0, 0002. Найти вероятность того, что на базу прибудут 3 негодные изделия.

Решение. 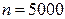, , 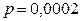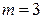. Тогда 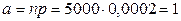, следовательно,

.

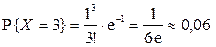Ответ: .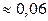

Наиболее вероятное значение, т.е. мода , случайной величины 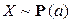удовлетворяет неравенству

,

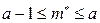которое следует из неравенства 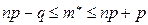для случайной величины 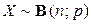при выполнении условий теоремы Пуассона.

Замечание. Имеются специальные таблицы, с помощью которых можно найти 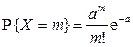, зная m и a.

Пример 2.1.29. В стае 1000 птиц, из которых 50 окольцованных. Орнитологами поймано 100 птиц. Каково среднее число окольцованных птиц среди пойманных? Какова вероятность того, что среди пойманных птиц нет окольцованных?

Решение. Орнитологами произведено 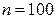независимых «опытов» (под «опытом» понимается поимка одной птицы из стаи) с одинаковой вероятностью «успеха» (под «успехом» понимается поимка окольцованной птицы) 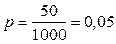. Поскольку n достаточно велико, p – мала, а произведение 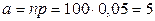удовлетворяет условию 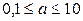, то можно считать, что случайная величина X – количество окольцованных птиц среди пойманных – распределена по закону Пуассона. Тогда среднее число окольцованных птиц среди пойманных, т.е. математическое ожидание 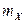, равно 5 (в распределении Пуассона ). Далее

.

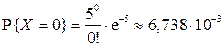Ответ: 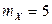; .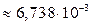