
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Упражнения. Биномиальное распределение
|
|
Биномиальное распределение
2.1.16. Вероятность брака при производстве приборов составляет 10%. С какой вероятностью среди 6 приборов, взятых для контроля, окажется ровно 2 бракованных?
2.1.17. Студент может правильно решить задачу из контрольной работы с вероятностью 0, 3. Какова вероятность того, что из предложенных шести задач варианта он решит ровно 4 задачи?
2.1.18. Из колоды в 36 карт 7 раз подряд наудачу выбирают карту, всякий раз возвращая её в колоду. С какой вероятностью ровно 5 из выбранных карт будут пиковой масти?
2.1.19. В урне 6 белых и 4 черных шара. Из нее пять раз подряд извлекают шар, причем каждый раз вынутый шар возвращают в урну и шары перемешивают. Приняв за случайную величину Х число извлеченных белых шаров, составить закон распределения этой величины, определить ее математическое ожидание, дисперсию и моду.
2.1.20. Рабочий обслуживает четыре одинаковых станка. Вероятность того, что в течение часа станок потребует регулировки, равна 0, 25. Приняв за случайную величину Х число станков, которое придется регулировать в течение часа рабочему, составить закон распределения этой величины, определить ее математическое ожидание, дисперсию и моду.
2.1.21. В магазин зашли четверо лиц. Вероятность того, что любой из посетителей не уйдет без покупки, равна 0, 3. Приняв за случайную величину Х число лиц, совершивших покупку, составить закон распределения этой величины, определить ее математическое ожидание, дисперсию и моду.
2.1.22. В урне 20 белых и 10 черных шаров. Вынули подряд четыре шара, причем каждый вынутый шар возвращают в урну перед извлечением следующего и шары в урне перемешивают. Приняв за случайную величину Х число извлеченных белых шаров, составить закон распределения этой величины, определить ее математическое ожидание, дисперсию и моду.
2.1.23. Заявки, рассылаемые фирмой, удовлетворяются примерно в 30% случаев независимо друг от друга. Фирма разослала 12 заявок. Найти математическое ожидание и дисперсию числа удовлетворенных заявок X, а также 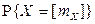 , где
, где 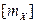 – целая часть числа
– целая часть числа 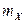 .
.
2.1.24. Случайным образом из колоды карт (36 карт) последовательно выкладывают на стол карты лицевой стороной вверх. На карты первой колоды таким же образом кладут сверху карты второй колоды (36 карт). Найти среднее число совпадений карт верхней и нижней колоды.
Распределение Пуассона
2.1.25. Среди семян ржи имеется 0, 04% семян сорняков. Какова вероятность при случайном отборе 5000 семян обнаружить 5 семян сорняков?
2.1.26. Учебник издан тиражом 100 000 экземпляров. Вероятность того, что учебник сброшюрован неправильно, равна 0, 00004. Найти вероятность того, что тираж содержит ровно пять бракованных книг.
2.1.27. Супермаркет получил 10 000 бутылок минеральной воды. Вероятность того, что при перевозке бутылка окажется разбитой, равна 0, 0003. Найти вероятность того, что супермаркет получит не менее двух разбитых бутылок.
2.1.28. Автоматическая телефонная станция получает в среднем за час 300 вызовов. Какова вероятность того, что за данную минуту она получит не более одного вызова?
2.1.29. В магазин за покупками приходят в среднем 30 человек в час. С какой вероятностью в течение минуты в магазин не войдёт ни один покупатель?
2.1.30. На регистрирующее устройство попадает в среднем 120 космических частиц в минуту. С какой вероятностью за одну секунду будет зарегистрировано не менее двух частиц?
2.1.31. Коммутатор в течение часа получает в среднем 60 вызовов. Телефонистка отлучилась на 30 секунд. С какой вероятностью за это время на коммутатор придёт хотя бы один вызов?
2.1.32. Вероятность изготовления бракованного сверла равна 0, 02. Свёрла укладываются в коробки по 100 штук. Воспользовавшись теоремой Пуассона, определить вероятность того, что количество бракованных свёрл в коробке не превышает двух.
Геометрическое распределение
2.1.33. Вероятность изготовления бракованной детали на станке равна 0, 05. Пусть X – число бракованных деталей, изготавливаемых на станке с начала его работы до появления первой бракованной детали. Найти 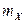 и
и  .
.
2.1.34. Из колоды, состоящей из 36 карт, последовательно достают по одной карте, каждый раз возвращая обратно. Найти среднее число извлеченных карт до появления туза пик и вероятность того, что до появления туза пик придется извлекать не менее 3 карт.
2.1.35. При проведении операции срочно потребовался донор с редкой группой крови. По статистике такая группа крови встречается у 5% людей. Сколько в среднем придется опросить людей, чтобы найти человека с такой группой крови? Какова вероятность того, что из 10 сотрудников, работающих в операционной, найдется хотя бы один с такой группой крови?
Ответы к упражнениям
2.1.16. 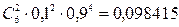 .
.
2.1.17. 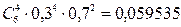 .
.
2.1.18. 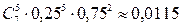 .
.
2.1.19.
| Х | ||||||
| P | 0, 01024 | 0, 0768 | 0, 2304 | 0, 3456 | 0, 2592 | 0, 07776 |
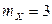 ,
, 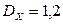 ,
, 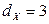 .
.
2.1.20.
| Х | |||||
| P | 
| 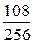
| 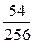
| 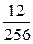
| 
|
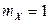 ,
, 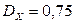 ,
, 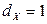 .
.
2.1.21.
| Х | |||||
| P | 0, 2401 | 0, 4116 | 0, 2646 | 0, 0756 | 0, 0081 |
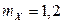 ,
, 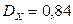 ,
, 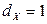 .
.
2.1.22.
| Х | |||||
| P | 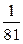
| 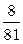
| 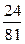
| 
| 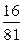
|
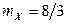 ,
,  ,
, 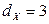 .
.
2.1.23. 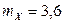 ,
, 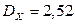 ,
,  .
.
2.1.24. 1.
2.1.25.  .
.
2.1.26.  .
.
2.1.27. 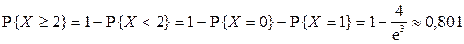 .
.
2.1.28. 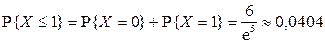 .
.
2.1.29. 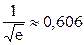 .
.
2.1.30. 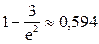 .
.
2.1.31. 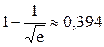 .
.
2.1.32. 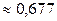 .
.
2.1.33. 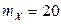 ;
; 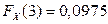 .
.
2.1.34. 36 карт; 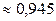 .
.
2.1.35. 20 человек; 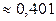 . Указание. При ответе на первый вопрос задачи используется «геометрическое + 1» распределение, а при ответе на второй вопрос применяется биномиальное распределение.
. Указание. При ответе на первый вопрос задачи используется «геометрическое + 1» распределение, а при ответе на второй вопрос применяется биномиальное распределение.