
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Показательное (экспоненциальное) распределение
|
|
Определение. СВНТ Х имеет показательное (экспоненциальное) распределение с параметром 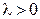 , если плотность вероятности имеет вид
, если плотность вероятности имеет вид


График плотности 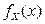 приведен на рис. 2.1.12.
приведен на рис. 2.1.12.
Замечание. Это распределение зависит от одного параметра – 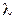 , поэтому пишут
, поэтому пишут  .
.
 Функция распределения
Функция распределения  :
:
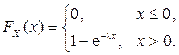
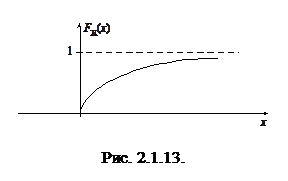
График  приведен на рис. 2.1.13.
приведен на рис. 2.1.13.
Медиана  равна
равна  .
.
Математическое ожидание, дисперсия и среднее квадратическое отклонение  равны:
равны:
 ,
,  ,
, 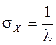 .
.
Замечание. Среднее квадратическое отклонение  совпадает с математическим ожиданием.
совпадает с математическим ожиданием.
Показательное распределение тесно связано с простейшим (стационарным пуассоновским) потоком событий.
Пример 2.1.36. Показать, что интервал времени Т между двумя соседними событиями в простейшем потоке имеет показательное распределение с параметром 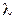 , равным интенсивности потока:
, равным интенсивности потока: 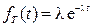 (
(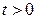 ).
).
Решение. Найдем вначале  . Рассмотрим на оси 0 t интервал времени T между двумя соседними событиями потока (рис. 2.1.14).
. Рассмотрим на оси 0 t интервал времени T между двумя соседними событиями потока (рис. 2.1.14).

Рис. 2.1.14.
Для того чтобы выполнялось неравенство  , нужно, чтобы хотя бы одно событие потока попало на участок длины t. Вероятность этого:
, нужно, чтобы хотя бы одно событие потока попало на участок длины t. Вероятность этого:
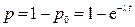 .
.
Отсюда функция распределения: 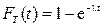 (
(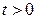 ). Дифференцируя
). Дифференцируя 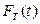 , получим плотность вероятности
, получим плотность вероятности 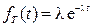 (
(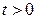 ), а это есть не что иное, как показательное распределение.
), а это есть не что иное, как показательное распределение.
Замечание. Показательное распределение играет большую роль в теории марковских случайных процессов, теории массового обслуживания и теории надежности.
Пример 2.1.37. Время безотказной работы ЭВМ – случайная величина Т, имеющая показательное распределение с параметром 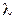 (физический смысл
(физический смысл 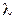 – среднее число отказов в единицу времени, если не учитывать простоев ЭВМ). Известно, что ЭВМ уже проработала без отказов время
– среднее число отказов в единицу времени, если не учитывать простоев ЭВМ). Известно, что ЭВМ уже проработала без отказов время 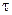 . Найти при этом условии плотность распределения
. Найти при этом условии плотность распределения 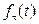 времени
времени 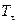 , которое ЭВМ проработает после момента
, которое ЭВМ проработает после момента 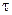 до ближайшего отказа.
до ближайшего отказа.
Решение. Так как простейший поток отказов не имеет последействия, то вероятность появления хотя бы одного отказа на участке  не зависит от того, появлялись ли отказы ранее момента
не зависит от того, появлялись ли отказы ранее момента 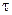 :
: 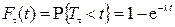 (рис. 2.1.15). Откуда
(рис. 2.1.15). Откуда  (
(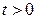 ).
).

Рис. 2.1.15.
Таким образом, распределение времени, оставшегося до следующего отказа, не зависит от того, сколько времени ЭВМ уже проработала безотказно.
Пример 2.1.38. Случайная величина распределена по показательному закону 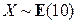 . Вычислить вероятность
. Вычислить вероятность 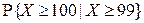 .
.
Решение. Воспользуемся определением условной вероятности:
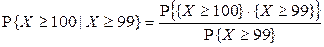 .
.
Поскольку событие 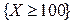 влечет событие
влечет событие  , т.е.
, т.е. 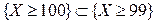 , то
, то 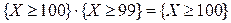 . Следовательно,
. Следовательно,
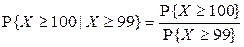 .
.
Переходя в числителе и знаменателе к противоположным событиям, получим:
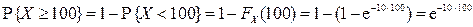 ,
,
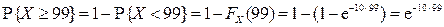 .
.
Таким образом,
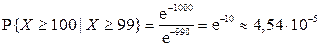 .
.
Ответ: 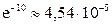 .
.
Пример 2.1.39. Время ремонта и обслуживания автомобиля после одной поездки случайно и удовлетворительно описывается экспоненциальным законом распределения. Было замечено, что в текущем сезоне на ремонт и обслуживание автомобиля после одной поездки тратилось в среднем 5 минут. Найти вероятность того, что при очередной поездке это время не превысит 30 минут.
Решение. Пусть X – время ремонта и обслуживания автомобиля после одной поездки. По условию задачи  и
и 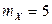 . Поскольку
. Поскольку  , то
, то 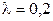 . Плотность вероятности
. Плотность вероятности  имеет вид:
имеет вид:

Требуется найти  . Следовательно, получаем
. Следовательно, получаем
 .
.
Ответ: 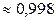 .
.
Пример 2.1.40. Опытами установлено, что в течение месяца выходит из строя 0, 02% электрических лампочек определенного типа. Человек для своей новой трехламповой люстры купил три лампочки этого типа. Какова вероятность того, что в течение 5 месяцев ему не понадобится новая лампочка (т.е. ни одна из лампочек в люстре не перегорит)?
Решение. Пусть X – время с момента начала подключения одной лампочки до того момента, как она перегорит. По условию задачи  и
и  . Найдем параметр
. Найдем параметр 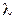 :
: 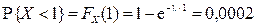 , или
, или 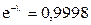 . Отсюда
. Отсюда 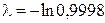 . Тогда вероятность, что одна лампочка не перегорит за 5 месяцев, равна
. Тогда вероятность, что одна лампочка не перегорит за 5 месяцев, равна
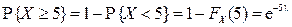 .
.
Поскольку время выхода из строя каждой из лампочек не зависит от времени выхода из строя других, то вероятность p того, что ни одна из лампочек в люстре не перегорит в течение 5 месяцев, равна
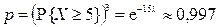 .
.
Ответ: 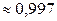 .
.