
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Равномерное распределение. Определение. СВНТ Х распределена равномерно на отрезке , если плотность вероятности имеет вид
|
|
Определение. СВНТ Х распределена равномерно на отрезке 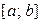 , если плотность вероятности имеет вид
, если плотность вероятности имеет вид
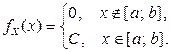
 График плотности
График плотности 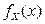 приведен на рис. 2.1.10.
приведен на рис. 2.1.10.
Замечание. Это распределение зависит от двух параметров – a и b, поэтому пишут 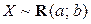 .
.
Из условия нормировки 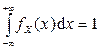 легко находится константа С:
легко находится константа С:
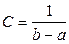 .
.
 Функция распределения
Функция распределения  случайной величины
случайной величины 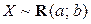 :
:
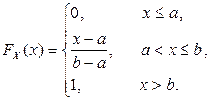
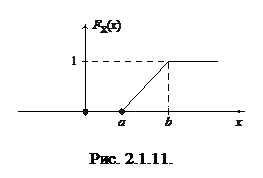
График  приведен на рис. 2.1.11.
приведен на рис. 2.1.11.
Математическое ожидание, дисперсия и среднее квадратическое отклонение  равны:
равны:
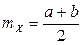 ,
, 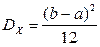 ,
, 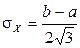 .
.
Моды равномерное распределение не имеет, а медиана совпадает с математическим ожиданием.
Пример 2.1.33. Случайная величина Х, являющаяся погрешностью приближенных вычислений каких-либо параметров при округлении до ближайших целых чисел, удовлетворительно описывается распределением 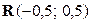 .
.
Пример 2.1.34. Случайная величина 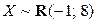 . Найти точку, в которой функция распределения равна
. Найти точку, в которой функция распределения равна  .
.
Решение. По определению функции распределения  . Тогда, согласно условию задачи
. Тогда, согласно условию задачи 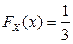 , или
, или  . Плотность вероятности имеет вид
. Плотность вероятности имеет вид
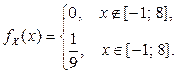
Получаем уравнение  , или
, или 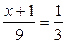 . Отсюда
. Отсюда 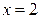 .
.
Заметим, что для решения этой задачи можно было сразу воспользоваться аналитическим выражением для функции распределения 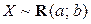
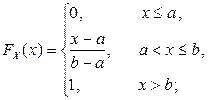
Тогда получится уравнение 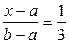 , в котором
, в котором 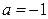 ,
, 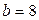 .
.
Ответ: 2.
Пример 2.1.35. Случайные величины имеют равномерное распределение 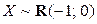 ,
, 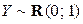 . Сравнить
. Сравнить  и
и  .
.
Решение. По условию задачи
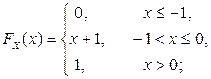

Тогда 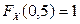 ,
, 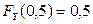 ,
, 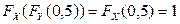 ,
, 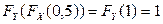 . Поэтому
. Поэтому  .
.
Ответ:  .
.