
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Нормальное распределение
|
|
Определение. СВНТ Х имеет нормальное (гауссовское) распределение с параметрами  и
и  , если плотность вероятности имеет вид
, если плотность вероятности имеет вид
 ,
,  .
.
Замечание. Это распределение зависит от двух параметров – m и s, поэтому пишут  .
.
 Методами математического анализа можно легко построить график плотности вероятности
Методами математического анализа можно легко построить график плотности вероятности 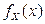 (кривой Гаусса) (рис. 2.1.16):
(кривой Гаусса) (рис. 2.1.16):
 Легко установить влияние параметров m и
Легко установить влияние параметров m и 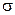 на вид кривой
на вид кривой 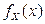 . Изменение m равносильно сдвигу кривой вдоль оси Ox. Причем в точке
. Изменение m равносильно сдвигу кривой вдоль оси Ox. Причем в точке 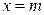 имеется единственный максимум функции
имеется единственный максимум функции 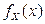 , равный
, равный  . Изменение
. Изменение 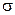 равносильно изменению масштаба кривой по обеим осям (например, при удвоении
равносильно изменению масштаба кривой по обеим осям (например, при удвоении 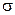 масштаб по оси Ox удвоится, а по оси Oy – уменьшится в два раза, при этом площадь под графиком
масштаб по оси Ox удвоится, а по оси Oy – уменьшится в два раза, при этом площадь под графиком 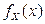 всегда равна единице) (рис. 2.1.17).
всегда равна единице) (рис. 2.1.17).
Общим называется нормальное распределение с параметрами m и s. Если случайная величина 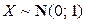 , то она называется стандартизованной нормальной случайной величиной. Ее плотность:
, то она называется стандартизованной нормальной случайной величиной. Ее плотность:
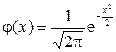 .
.
Эта функция табулирована только для  , поскольку является четной, т.е.
, поскольку является четной, т.е. 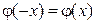 .
.
Математическое ожидание, дисперсия и среднее квадратическое отклонение  равны:
равны:
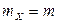 ,
,  ,
,  .
.
Таким образом, смысл параметров m и 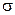 случайной величины
случайной величины  следующий:
следующий:
 .
.
Замечание. Поскольку график функции плотности 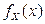 случайной величины
случайной величины  симметричен относительно прямой
симметричен относительно прямой 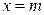 , то ответ
, то ответ 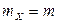 можно было получить сразу. Кроме того, мода и медиана случайной величины
можно было получить сразу. Кроме того, мода и медиана случайной величины  совпадают с ее математическим ожиданием и равны m.
совпадают с ее математическим ожиданием и равны m.
Функция распределения стандартизованной нормальной случайной величины имеет вид:
 .
.
Она часто называется функцией нормального распределения и также табулирована для  , поскольку
, поскольку
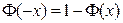 .
.
Кроме того, в этой таблице приведены значения функции  лишь для
лишь для  . Это обусловлено тем, что при
. Это обусловлено тем, что при 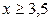 значения функции
значения функции  практически не отличается от единицы. Поэтому при решении задач можно считать, что
практически не отличается от единицы. Поэтому при решении задач можно считать, что 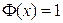 для
для 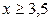 .
.
Функция распределения  для случайной величины
для случайной величины  связана функцией нормального распределения
связана функцией нормального распределения  при помощи формулы:
при помощи формулы:
 .
.
Поэтому очевидно, что
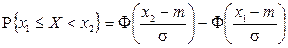 .
.
Пример 2.1.41. Дана случайная величина 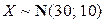 . Найти
. Найти 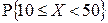 .
.
Решение. 
 .
.
Ответ: 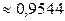 .
.
Часто требуется вычислить вероятность того, что отклонение случайной величины  от ее математического ожидания по абсолютной величине меньше заданного положительного числа e, т.е. требуется найти вероятность
от ее математического ожидания по абсолютной величине меньше заданного положительного числа e, т.е. требуется найти вероятность  . Задача решается так:
. Задача решается так:
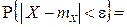
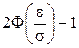 .
.
Случайная величина  с большой вероятностью принимает значения, близкие к своему математическому ожиданию, что описывается «правилом k сигм»:
с большой вероятностью принимает значения, близкие к своему математическому ожиданию, что описывается «правилом k сигм»:
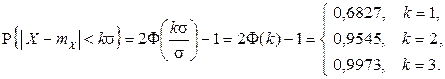
Пример 2.1.42. Рост взрослого мужчины удовлетворительно описывается нормальным законом распределения. По статистике средний рост составляет 180 см, а среднеквадратическое отклонение равно 7 см. Найти вероятность того, что рост наугад взятого мужчины будет отличаться от среднего роста менее чем на 7 см.
Решение. Обозначим рост наугад взятого взрослого мужчины через X. По условию задачи  . Требуется найти
. Требуется найти 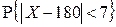 . Тогда
. Тогда
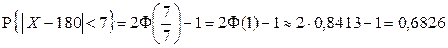 .
.
Ответ: 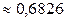 .
.
Пример 2.1.43. Случайная величина X имеет плотность вероятности
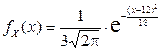 .
.
Какова вероятность того, что X попадет в интервал 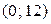 ? Чему равен второй начальный момент этой случайной величины?
? Чему равен второй начальный момент этой случайной величины?
Решение. Согласно условию задачи случайная величина имеет нормальное распределение  . Тогда
. Тогда
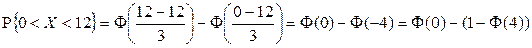 .
.
Поскольку 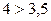 , то можно считать, что
, то можно считать, что  . Поэтому
. Поэтому
 .
.
Для нахождения второго начального момента 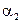 случайной величины
случайной величины  необходимо воспользоваться соотношением
необходимо воспользоваться соотношением  . По условию задачи
. По условию задачи 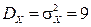 ,
, 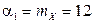 . Отсюда
. Отсюда
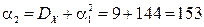 .
.
Ответ: 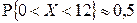 ,
, 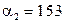 .
.
Пример 2.1.44. Считается, что отклонение длины изготавливаемых деталей от стандарта является случайной величиной, распределенной по нормальному закону. Если стандартная длина детали 40 см и среднее квадратическое отклонение равно 0, 4 см, то какую точность длины изделия можно гарантировать с вероятностью 0, 8?
Решение. По условию задачи случайная величина X – длина изготавливаемой детали – имеет нормальное распределение  . Требуется найти положительное число
. Требуется найти положительное число  , для которого
, для которого 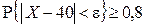 . Поскольку
. Поскольку 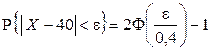 , то задача сводится к решению неравенства
, то задача сводится к решению неравенства 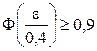 . По таблице квантилей нормального распределения
. По таблице квантилей нормального распределения 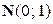 находим:
находим:  , или
, или 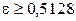 . Таким образом, наименьшее значение
. Таким образом, наименьшее значение  равно 0, 5128 см.
равно 0, 5128 см.
Ответ: 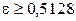 см.
см.
Пример 2.1.45. Пусть X – случайная величина, подчиненная нормальному закону  . Какова вероятность того, что при четырех испытаниях эта случайная величина хотя бы один раз попадет в интервал
. Какова вероятность того, что при четырех испытаниях эта случайная величина хотя бы один раз попадет в интервал  ?
?
Решение. Найдем вероятность попадания случайной величины X в интервал  при одном испытании:
при одном испытании:
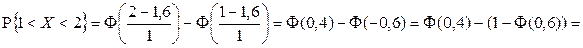
 .
.
Тогда вероятность того, что случайная величина не попадет в интервал  при одном испытании, равна
при одном испытании, равна 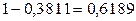 , а при четырех испытаниях
, а при четырех испытаниях  . Значит, искомая вероятность составляет
. Значит, искомая вероятность составляет 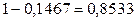 .
.
Ответ:  .
.