Упражнения

Равномерное распределение

2.1.36. Случайная величина X имеет равномерное распределение на отрезке 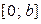. Известно, что 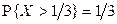. Найти b и начальный момент .

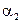2.1.37. Найти p -квантиль распределения .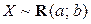

2.1.38. Если соблюдается график движения трамваев, то среднее время ожидания пассажиром трамвая равно 3, 5 минуты. Известно, что время ожидания имеет равномерный закон распределения. Минимальное время ожидания равно 0. Найти вероятность того, что пассажир будет ожидать трамвай от 2 до 5 минут.

2.1.39. Длина комнаты измеряется с помощью рулетки с грубыми делениями, отделенными расстояниями 10 см. Округление производится до ближайшего деления. Случайная величина X – ошибка измерения. Найти и построить функцию плотности распределения 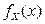, найти математическое ожидание и дисперсию случайной величины X.

2.1.40. Поезда данного маршрута городского трамвая идут с интервалом 5 минут. Пассажир подходит к трамвайной остановке в некоторый момент времени. Какова вероятность появления пассажира не ранее, чем через минуту после ухода предыдущего поезда, но не позднее, чем за две минуты до отхода следующего поезда?

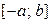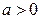2.1.41. Случайная величина X равномерно распределена на отрезке , где и 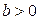. Вероятность того, что эта случайная величина примет отрицательное значение, равна 0, 75. Рассматривается другая случайная величина Y, равномерно распределенная на отрезке 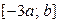. Чему равна вероятность того, что случайная величина Y будет отрицательной?

Показательное (экспоненциальное) распределение

2.1.42. Случайная величина X имеет показательное распределение 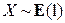. Вычислить 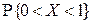. Сравнить 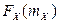и 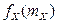, а также 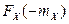и .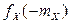

2.1.43. Найти p -квантиль распределения .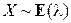

2.1.44. Время X безотказной работы станка имеет показательное распределение. Вероятность того, что станок не откажет за 5 часов работы, равна 0, 60653. Найти 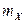, , начальный момент .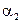

2.1.45. Вероятность того, что некий прибор проработает 1 час, равна 0, 9. Какова вероятность того, что прибор безотказно проработает сутки?

2.1.46. 98% топливных насосов дизельных тракторов выходят из строя после 3000 моточасов. Какова вероятность того, что насос выйдет из строя в интервале времени от 2000 до 2500 моточасов?

2.1.47. По данным страховых агентств некоторого государства вероятность того, что гражданин этой страны доживет до 70 лет, равна 0, 87. Какова вероятность того, что случайный новорожденный этой страны доживет до свадьбы, если по статистике этот возраст составляет 22 года?

2.1.48. Известно, что среднее время ожидания кассиром очередного покупателя, подошедшего к кассе, равно 0, 2 минуты. Время ожидания кассиром очередного покупателя можно считать случайной величиной, имеющей показательный закон распределения. Кассиру нужно сменить ленту кассового аппарата. На это ему требуется две минуты. Какова вероятность того, что за это время не образуется очередь, т.е. к кассе не подойдет ни один покупатель?

2.1.49. Блок прибора построен из трех независимых, параллельно действующих одинаковых элементов. Отказ блока происходит лишь в случае, когда отказывают все три элемента. Плотность распределения времени исправной работы X каждого из элементов равна . Какова вероятность того, что блок безотказно проработает 600 часов?

Нормальное распределение

2.1.50. Случайная величина . Сравнить и .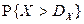

2.1.51. Случайная величина 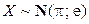. Вычислить .

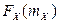2.1.52. Случайная величина X подчинена нормальному закону распределения. Второй начальный момент и второй центральный момент равны 14 и 10 соответственно. Чему равно значение функции распределения случайной величины X в точке ?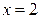

2.1.53. Деталь считается бракованной, если ее отклонение X от номинала больше 5 мм. Считая, что случайная величина Х распределена нормально со средним квадратическим отклонением 3 мм, установить процент годных деталей.

2.1.54. Мастерская изготавливает стержни, длина которых представляет собой случайную величину, распределенную по нормальному закону с математическим ожиданием 25 см и средним квадратическим отклонением 0, 1 см. Найти вероятность того, что отклонение длины стержня от среднего размера не превзойдет 0, 25 см.

2.1.55. Деталь считается бракованной, если ее отклонение X от номинала больше 4 мм. Считая, что случайная величина Х распределена нормально со средним квадратическим отклонением 2 мм, установить процент бракованных деталей.

2.1.56. Автомат изготавливает шарики. Шарик считается годным, если отклонение Х диаметра шарика от проектного размера по абсолютной величине меньше 0, 7 мм. Считая, что случайная величина Х распределена нормально со средним квадратическим отклонением 0, 4 мм, найти, сколько в среднем будет годных шариков среди 100 изготовленных.

2.1.57. Случайная величина . При каком x вероятность попадания случайной величины X в интервал равна 0, 7?

2.1.58. Случайная величина . Найти интервал, симметричный относительно математического ожидания, в который случайная величина X попадает с вероятностью 0, 5.

2.1.59. Случайная величина . Найти 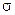, если известно, что вероятность .

2.1.60. Поезд состоит из 100 вагонов. Масса каждого вагона – случайная величина (измеряемая в тоннах), распределенная по нормальному закону 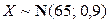. Локомотив может везти состав массой не более 6600 тонн, в противном случае необходимо прицеплять второй локомотив. Найти вероятность того, что второй локомотив не потребуется.

2.1.61. Диаметр выпускаемой детали – случайная величина (измеряемая в сантиметрах), распределенная по нормальному закону 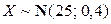. Найти вероятность того, что две взятые наудачу детали имеют отклонение от математического ожидания по абсолютной величине не более 0, 16 см.

2.1.62. Диаметр выпускаемой детали – случайная величина (измеряемая в сантиметрах), распределенная по нормальному закону 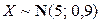. Установить: 1) вероятность того, что наудачу взятая деталь имеет диаметр в пределах от 4 до 7 см; 2) вероятность того, что размер диаметра наудачу взятой детали отличается от математического ожидания не более чем на 2 см; 3) в каких границах следует ожидать размер диаметра детали, чтобы вероятность не выйти за эти границы была равна 0, 95.

2.1.63. Случайная величина . Какова вероятность того, что при первом испытании случайная величина окажется на отрезке 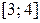, а при втором испытании – на отрезке ?

2.1.64. Случайная величина . Каково должно быть среднее квадратическое отклонение 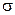этой случайной величины, чтобы с вероятностью 0, 8 отклонение от математического ожидания по абсолютной величине не превышало 0, 2?

Асимметрия и эксцесс

2.1.65. Дана функция плотности случайной величины X:

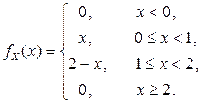
Найти асимметрию и эксцесс случайной величины X.

2.1.66. Случайная величина X подчинена закону распределения с плотностью 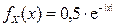. Найти асимметрию и эксцесс случайной величины X.

2.1.67. Найти асимметрию и эксцесс случайной величины, имеющей показательное распределение .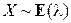

Ответы к упражнениям

2.1.36. , .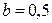

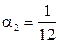2.1.37. .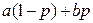

2.1.38. , , .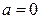

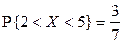2.1.39. , .

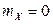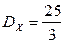2.1.40. 0, 4.

2.1.41. 0, 9.

2.1.42. , , .

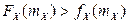2.1.43. .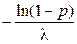

2.1.44. , , .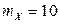

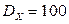2.1.45. .

2.1.46. .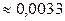

2.1.47. .

2.1.48. .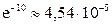

2.1.49. .

2.1.50. .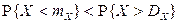

2.1.51. 0, 5.

2.1.52. 0, 5 или .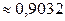

2.1.53. %.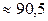

2.1.54. .

2.1.55. %.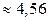

2.1.56. , .

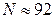2.1.57. .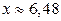

2.1.58. .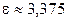

2.1.59. .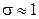

2.1.60. .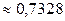

2.1.61. .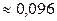

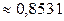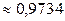2.1.62. 1) ; 2) ; 3) .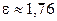

2.1.63. .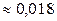

2.1.64. .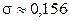

2.1.65. , .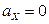

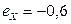2.1.66. , .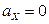

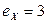2.1.67. , .