Мода, медиана и квантили

Математическое ожидание не единственная характеристика положения, применяемая в теории вероятностей. Часто применяются и другие, например, мода и медиана.

Определение. Модой 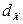СВДТ Х называется такое ее возможное значение 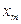, для которого 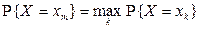, т.е. .

Модой СВНТ Х называется действительное число 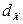, являющееся точкой максимума функции плотности .

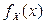Пример 2.1.21. Закон распределения случайной величины X имеет вид:

Тогда .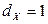

Замечание. Мода может не существовать, иметь единственное значение (такие распределения называются унимодальными) или иметь множество значений (полимодальные распределения). Наличие более чем одной моды, часто указывает на разнородность статистического материала, который был положен в основу исследования.

Пример 2.1.22. Дана плотность вероятности СВНТ X 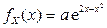(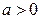). Найти моду этой случайной величины.

Решение. Функция плотности 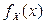определена и дифференцируема на 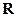. Найдем точку максимума 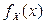. Для этого возьмем ее производную:

.

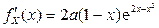Критические точки находятся из условия 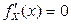: , или 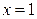. Очевидно, что (рис. 2.1.9):

Рис. 2.1.9.

Таким образом, 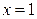– точка максимума функции 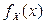, т.е. .

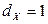Заметим, что определять значения константы a не нужно, т.к. при 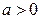максимум функции не зависит от ее числового значения.

Ответ: .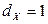

Определение. Медианой случайной величины Х называется действительное число , удовлетворяющее условию .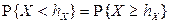

Таким образом, медиана – корень уравнения .

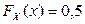Замечания. 1) Эта характеристика применяется, как правило, только для СВНТ, и геометрически медиана – это абсцисса той точки на оси Оx, для которой площади под графиком функции плотности 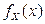, лежащие слева и справа от нее, одинаковы и равны 0, 5.

2) В случае симметричного распределения (имеющего моду) три характеристики – математическое ожидание (если оно существует), мода и медиана совпадают.

3) Уравнение 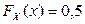может иметь множество корней, поэтому медиана может определяться неоднозначно.

Пример 2.1.23. Дана плотность распределения случайной величины Х:

Найти моду и медиану случайной величины Х.

Решение. Очевидно, что распределение симметрично, т.к. график плотност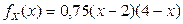и при 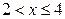является параболой. Осью симметрии является вертикальная прямая 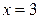. Поэтому .

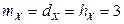Ответ: .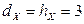

Пример 2.1.24. Дана плотность распределения случайной величины Х:

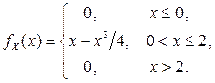
Найти моду и медиану случайной величины Х.

Решение. 1) Найдем вначале моду СВНТ X. Очевидно, что точку максимума функции 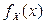следует искать на интервале 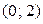. Плотность 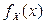определена и дважды дифференцируема для всех . Найдем на этом интервале производные первого и второго порядков:

, .

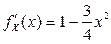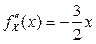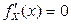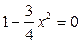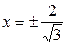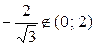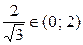Критические точки находятся из условия : , или . Поскольку , а , то 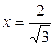– единственная критическая точка. Так как , то 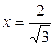– точка максимума плотности распределения. Значит, .

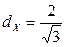2) Очевидно, что медиану следует искать на интервале 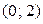. Для ее нахождения можно вначале составить функцию распределения, а затем решить уравнение 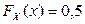. Однако проще поступить следующим образом:

.

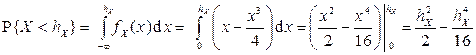По определению медианы 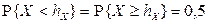, поэтому получаем уравнение:

, или 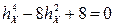, откуда .

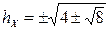Из четырех корней этого уравнения только один 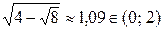, поэтому .

Ответ: , .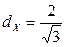

Определение. Квантú лью порядка р распределения СВНТ Х называется действительное число 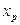, удовлетворяющее условию .

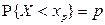Замечание. Медиана 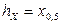, т.е. – квантиль порядка 0, 5.

Пример 2.1.25. Найти квантиль порядка 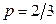для СВНТ X, имеющей плотность вероятности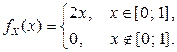

Решение. На отрезке 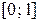функция распределения СВНТ X имеет вид

, ,

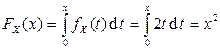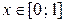и поэтому является непрерывной и строго монотонной на отрезке 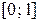. В соответствии со свойством квантили находим 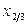из уравнения 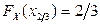. Откуда .

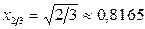Ответ: 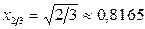.