
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Математическое ожидание дискретной случайной величины
|
|
Пусть ДСВ X имеет закон распределения:
| X | x1 x2 x3 … xn |
| P | p1 p2 p3 … pn |
Математическим ожиданием (МО) дискретной случайной величины называется сумма произведений всех ее возможных значении на их вероятности: 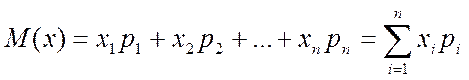 (6)
(6)
Из этого определения следует, что МО есть некоторая постоянная неслучайная величина. Вероятностный смысл математического ожидания состоит в том, что оно приближенно равно среднему арифметическому значению случайной величины. МО в точности совпадает со средним арифметическим, если все вероятности значений ДСВ в формуле (6) равны, а именно, рi = р= 1/ п
Пример 4. Найти МО невозврата кредитов по данным примера 2.
Решение. Воспользуемся итоговой таблицей распределения ДСВ, данной в этом примере и формулой (6):
M (X) = 5 . 0, 00032 + 4 . 0, 0064 + 3 . 0, 0512
+ 2 . 0, 2048 + 1 . 0, 4096 + 0 . 0, 32768 = 1
Основные свойства математического ожидания:
1. Математическое ожидание постоянной величины С равно С:
M (С) = С (7)
2. Постоянный множитель можно выносить за знак математического ожидания:
М (сХ) = сМ (Х) (8)
3. Математическое ожидание суммы случайных величин равно сумме их математических ожиданий:
М (Х1 + Х2 + … + Хm) = М (Х1) + М (Х2) + … + М (Хm) (9)
4. Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий
М (Х1 Х2 … Хm) = М (Х1) М (Х2) … М (Хm) (10)
Пример 5. Пусть ежедневные расходы на обслуживание и рекламу автомобилей в автосалоне составляют в среднем 120 тыс. ден. ед., а число продаж Х автомашин в течение дня подчиняется закону распределения
| Х | ||||||||||
| P | 0, 25 | 0, 2 | 0, 1 | 0, 1 | 0, 1 | 0, 1 | 0, 05 | 0, 05 | 0, 025 | 0, 025 |
Найти МО ежедневной прибыли при цене машины в 150 тыс. ден.ед.
Решение. Очевидно, что ежедневная прибыль подсчитывается по формуле:
П = 150 Х – 120
Искомое МО находится с использованием указанных ранее свойств математического ожидания (в тыс. ден. ед.):
М (П) = М (150 Х – 120) = 150 М (Х) – 120 = 150 . 2, 675 – 120 = 281, 25