Числовые характеристики непрерывных случайных величин

Определения числовых характеристик дискретных случайных величин распространяются и на непрерывные величины. Разница состоит лишь в том, что вместо сумм в соответствующих формулах берутся их интегральные аналоги.

Формулы для математического ожидания и дисперсии НСВ:

М (X)= 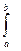x ƒ (x) dx, D (X)= 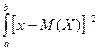ƒ (x) dx (39)

В том случае, когда возможные значения случайной величины X заполняют всю ось Оx, то пределы интегрировании a и b бесконечны: a = - ∞, b = ∞. Возможны также случаи, когда один из пределов интегрирования бесконечен (возможные значения X лежат на полупрямой).

Среднее квадратическое отклонение НСВ определяется, как и прежде, по формуле:

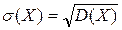
Для вычисления дисперсии употребляется более удобная формула:

(40)

Пример 9. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины X, заданной плотностью распределения на отрезке [ 0, 1 ]:

ƒ (x) = 1, x 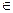[ 0, 1 ]

Решение. Согласно формулам (39), (40), последовательно вычисляем искомые величины:

М (X) = 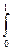x ƒ (x) dx = 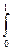x dx = .