Коэффициент корреляции

Корреляционным моментом случайных величин X и Y или ковариацией называется математическое ожидание произведений их отклонений от математического ожидания случайных величин X и Y: (20)

Корреляционный момент служит для описания связи между случайными величинами X и Y. Из свойств математического ожидания легко убедиться в том, что можно записать в следующем виде:

(21)

или

Из формулы (21) следует, что корреляционный момент двух независимых случайных наличии равен нулю, так как для независимых СВ

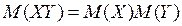
Если корреляционный момент 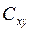не равен нулю, то величины X и Y являются зависимыми.

Коэффициентом корреляции случайных величин X и Y называется отношение их корреляционного момента к произведению средних квадратических отклонений этих величин:

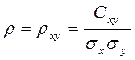(22)

Коэффициент корреляции является безразмерным и не зависит от выбора системы измерения случайных величин, а его абсолютная величина не превосходит единицы:

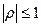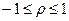или (23)

Две случайные величины X и Y называется коррелированными. если их корреляционный момент (коэффициент корреляции) отличен от нуля. Если же их корреляционный момент равен нулю, то X и Y называются некоррелированными. Таким образом, две коррелированные случайные величины (т.е. при ) являются также и зависимыми. Обратное утверждение неверно, т.е. две зависимые величины могут быть как коррелированными, так и некоррелированными