Определение усилий и построение ЛВ в элементах простых ферм. 4. 2. Определение усилий в стержнях простейших ферм

Фермы, образованные из шарнирного треугольника путем последовательного присоединения узлов (причем каждого с помощью двух стержней, не лежащих на одной прямой), называются простейшими. Такие фермы геометрически неизменяемы и статически определимы (см. § 1.2 и 1.3).

В § 1.3 было указано, что для любой статически определимой фермы можно составить уравнений статики (где К — число узлов фермы), с помощью которых можно найти опорные реакции и внутренние усилия (продольные силы) в ее стержнях от действия внешней нагрузки. При этом в первую очередь обычно определяют опорные реакции. При определении реакций составляют три уравнения равновесия для всей фермы в целом.

Для определения внутренних усилий следует выделять сечениями узлы или отдельные части фермы и рассматривать условия их равновесия под действием внешних нагрузок и усилий в рассеченных стержнях. Всего можно составить таких условий (т. е. независимых друг от друга уравнений).

Выделение узлов или частей фермы необходимо производить так, чтобы усилия в элементах фермы определялись наиболее просто, по возможности без совместного решения системы уравнений со многими неизвестными. Это позволяет не только значительно упростить расчет, но и получить более точные результаты.

Ниже излагаются способы расчета, позволяющие определить внутреннее усилие в каждом из элементов фермы, как правило, с помощью одного уравнения с одним неизвестным.

Способ момеитной точки. Способ моментной точки применяется главным образом в тех случаях, когда удается рассечь ферму на две части так, чтобы при этом перерезанными оказались три ее стержня, направления осей которых не пересекаются в одной точке (см., например, сечение 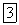на рис. 4.9, слева) 1. Направления осей трех таких перерезанных стержней пересекаются попарно в трех точках, не лежащих на одной прямой (рис. 4.9, справа).

Составляя последовательно уравнения моментов всех сил (внешних и внутренних), действующих на отсеченную часть фермы, относительно

этих трех точек, будем каждый раз получать уравнение с одним неизвестным, представляющим собой усилие в рассеченном стержне, не проходящем через рассматриваемую точку пересечения стержней.

Таким образом, для определения усилия в каком-либо стержне необходимо разрезать ферму так, чтобы в разрез кроме данного стержня попали еще два других (оси которых не сходятся с ним в общей точке), после чего из уравнения моментов относительно точки пересечения осей этих двух стер жней, можно легко определить усилие в данном стержне.

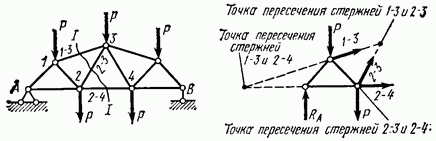
Рис. 4.9

Точка пересечения осей двух стержней, относительно которой составляется уравнение моментов, называется моментной.

При составлении уравнений равновесия все неизвестные усилия в стержне фермы условно считаются положительными, т. е. растягивающими и, следовательно, направленными от узлов. Если после решения уравнений какое-либо усилие окажется отрицательным, то, значит, оно является сжимающим и направлено к узлу.

Рис. 4.10

Перейдем к примерам расчета, поясняющим способ моментной точки.

Условимся усилия в элементах верхнего пояса фермы обозначать буквой О, усилия в элементах нижнего пояса — буквой U, усилия в раскосах — буквой D, усилия в стойках — буквой V. У этих букв внизу будем ставить цифры, соответствующие узлам фермы, к которым присоединен данный стержень.

Рассмотрим ферму, изображенную на рис. 4.10, а. Найдем усилие в стержне 3—5. Для этого рассечем ферму по линии пересекающей

рассматриваемый стержень 3—5 и два других. Разрезав таким образом ферму на две части, одну из них отбросим и рассмотрим условие равновесия другой части.

Всегда проще рассматривать ту часть фермы, на которую действует меньше сил, а потому в данном случае рассмотрим ее левую часть. Она должна оставаться в равновесии под действием внешних сил 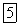и внутренних усилий и в рассеченных элементах; эти усилия заменяют собой действие отброшенной правой части фермы на левую (рис. 4.10, б).

Для определения неизвестного усилия с помощью одного уравнения с одним неизвестным составим сумму моментов всех сил, действующих на левую часть фермы, относительно точки пересечения рассеченных стержней 2—4 и 3—4, т. е. точки 4. Эта точка при определении усилия в стержне 3—5 будет моментной точкой.

Сумма моментов всех сил, действующих на левую часть фермы, относительно точки 4 имеет вид

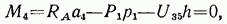
откуда

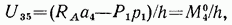
где h — плечо усилия относительно моментной точки, равное в данном случае высоте фермы; — момент всех внешних (включая и опорную реакцию) сил, приложенных к выделенной части фермы, относительно узла 4, равный изгибающему моменту в простой балке в сечении, соответствующем положению моментной точки.

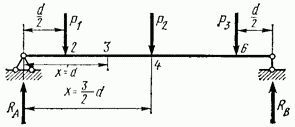
Рис. 4.11

В самом деле, если данную ферму с действующей на нее вертикальной нагрузкой заменить простой балкой того же пролета (рис. 4.11), то изгибающий момент в ее сечении с абсциссой, равной абсциссе моментной точки 4, будет равен моменту сил, приложенных к левой отсеченной части фермы, относительно этой точки.

Таким образом, усилие в элементе нижнего пояса фермы равно отношению изгибающего (балочного) момента в соответствующем сечении простой балки к плечу

Так как изгибающий момент в балке при любой нагрузке, действующей сверху вниз, всегда положителен, то усилие также всегда положительно, т. е. стержень 3—5 растянут. При заданной нагрузке все остальные стержни нижнего пояса фермы также растянуты.

Определим усилие в элементе 2—4 верхнего пояса фермы. Для этого составим выражение момента всех сил, действующих на отсеченную левую часть фермы, относительно моментной точки (т. е. узла 3, см. рис. 4.10, б):

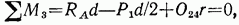
откуда

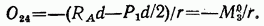
Числитель дроби, обозначенный равен изгибающему моменту простой балки (см. рис. 4.11) в сечении с абсциссой Так как «балочный» момент при действии заданной нагрузки всегда положителен, а перед отношением в формуле стоит знак минус, то усилие отрицательно, т. е. элемент 2—4 сжат.

Аналогичным путем можно доказать, что все элементы верхнего пояса фермы при нагрузке, действующей сверху вниз, будут сжаты.

Для определения усилия возникающего в раскосе 3—4, составим выражение момента всех сил относительно точки k, расположенной вне контура фермы (см. рис. 4.10, б), в которой пересекаются оси стержней 2—4 и 3—5:

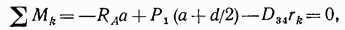
откуда

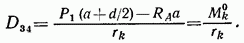
Итак, при применении способа моментной точки числовая величина усилия определяется выражением

Здесь М представляет собой момент сил, действующих на отсеченную часть фермы, относительно моментной точки, плечо искомого усилия относительно той же точки.

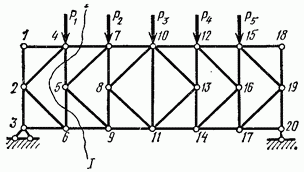
Рис. 4.12

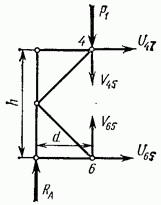
Рис. 4.13

При определении усилий в элементах верхнего или нижнего пояса более сложной фермы (из числа простейших ферм), изображенной на рис. 4.12, также можно применить способ моментной точки. В самом деле, если разрезать ферму по линии I—I и составить выражение суммы моментов сил, действующих на ее левую часть (рис. 4.13), относительно узла 6, в котором сходятся три из четырех перерезанных стержней, то полученное таким образом уравнение с одним неизвестным

известным даст возможность определить усилие в стержне 4-7:

откуда

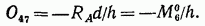
Для определения усилия в стержне 6—9 нижнего пояса фермы составим уравнение моментов сил относительно точки

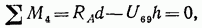
откуда

На рис. 4.14 изображена сложная ферма (также относящаяся к категории простейших), усилия в поясах которой тоже могут быть найдены способом моментной точки.

Рис. 4.14

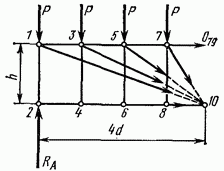
Рис. 4.15

Для определения усилия в стержне 7—9 сделаем разрез пересекающий кроме данного стержня еще пять стержней, сходящихся в одной общей точке (в узле 10). Составим выражение суммы моментов всех сил, действующих на отсеченную левую часть фермы (рис. 4.15), относительно этой точки:

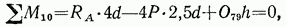
откуда

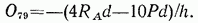
Рассмотрим еще так называемую ферму сетчатого покрытия, предложенную В. Г. Шуховым для перекрытия одного из больших зданий в Москвё (рис. 4.16) 1.

Эта ферма геометрически неизменяема, так как состоит из двух основных треугольников: 1—4—5 и 2—3—6, соединенных между собой тремя стержнями 1—2, 3—4 и 5—6, оси которых не пересекаются в одной общей точке. Ферма статически определима, так как число ее стержней S удовлетворяет условию а именно: . Ферма Шухова интересна тем, что для нее нельзя провести разрез, пересекающий только три стержня или же

какое-либо другое число стержней, так, чтобы все, за исключением одного, пересекались в одной точке.

Для расчета этой фермы проведем замкнутое сечение так, чтобы оно перерезало стержни 1—2, 3—4 и 5—6 по одному разу, а стержни 1—4 и 1—5 — по два раза.

Рис. 4.16

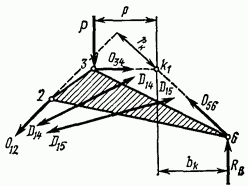
Рис. 4.17

Как видно из рис. 4.17, выделенные части дважды перерезанных стержней 1—4 и 1—5 будут уравновешены усилиями, приложенными по их концам: останутся только три неизвестных усилия: которые легко определить способом моментной точки.

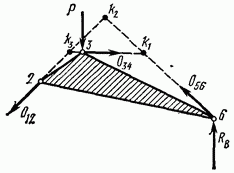
Рис. 4.18

Для определения усилия в стержне 1—2 составим сумму моментов всех сил, действующих на выделенную сечением часть фермы, относительно точки пересечения направлений стержней 3—4 и 5—6, т. е. точки (рис. 4.17):

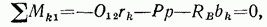
откуда

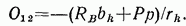
Моментной точкой при определении усилия будет точка пересечения направлений стержней 1—2 и 5— 6, т. е. точка а при определении усилия -точка (рис. 4.18).

Таким образом, усилия определяются независимо друг от друга с помощью трех уравнений, каждое из которых содержит по одному неизвестному.

Усилия в остальных стержнях могут быть определены с помощью сечений, пересекающих любое число стержней, если при этом неизвестны усилия не более чем в трех рассеченных стержнях.

На основании рассмотренных примеров можно сделать следующие выводы:

1. Способом моментной точки удобно пользоваться при расчете ферм, когда можно провести разрез, пересекающий кроме данного стержня (усилие в котором определяется) любое число стержней, сходящихся в одной общей точке, не лежащей на направлении оси данного стержня.

2. Способ моментной точки удобен также и в случаях, когда разрез пересекает более трех стержней, не сходящихся в одной точке, если усилия во всех стержнях, кроме трех, уже известны.

3. Способ моментной точки применим и для расчета таких ферм, в которых возможно провести разрезы, пересекающие любое число стержней сверх трех, если при этом каждый добавочный стержень пересекается дважды.

Как видно, при расчетах ферм по способу моментной точки каждое усилие определяется с помощью одного уравнения с одним неизвестным.

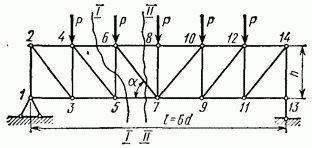
Рис. 4.19

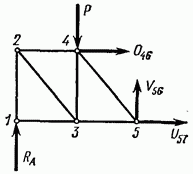
Рис. 4.20

При этом уравнение моментов составляется таким образом, что в состав его входят только действующие на ферму внешние силы и одно определяемое усилие в рассчитываемом элементе. В этих случаях возможная ошибка при определении усилия в одном элементе не оказывает влияния на усилие в другом элементе.

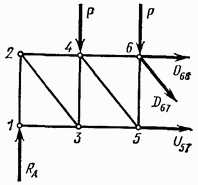
Рис. 4.21

Способ проекций. Способ проекций применяется главным образом в следующих двух вариантах:

1) рассматривается равновесие части фермы (как и при способе моментной точки), когда два из трех рассеченных стержней параллельны друг другу;

3) рассматривается равновесие выделяемых из фермы узлов (способ вырезания узлов) 1.

Определим усилия в элементах решетки фермы, изображенной на рис. 4.19.

Для определения усилия разрежем ферму сечением пересекающим стержни 4—6, 5—6 и 5—7. Так как моментная точка для усилия вследствие параллельности стержней 4—6 и 5—7 находится в бесконечности, то составить уравнение моментов относительно этой точки невозможно. Поэтому составим условие равновесия в виде суммы проекций всех сил, действующих на отсеченную часть фермы (рис. 4.20), на ось, перпендикулярную ее поясам (в это уравнение усилия в поясах не войдут, так как они перпендикулярны

оси проекций):

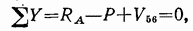
откуда

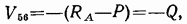
где Q — поперечная сила в простой балке.

Для определения усилия разрежем ферму по линии II—II (см. рис. 4.19) и составим уравнение равновесия для левой ее части (рис. 4.21):

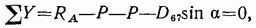
откуда

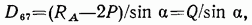
где Q — поперечная сила в простой балке, равная

При расчете простейших ферм все усилия можно определить способом проекций, применяя его последовательно к каждому узлу. При этом определение усилий надо начинать с узла, в котором сходится не более двух стержней.

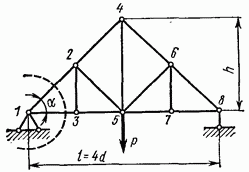
Рис. 4.22

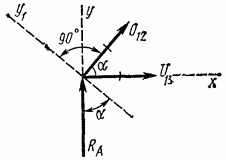
Рис. 4.23

Для примера определим усилия в стержнях 1—2, 1—3, 2—3 и 3—5 фермы, изображенной на рис. 4.22. Вырежем сначала левый опорный узел (рис. 4.23) и рассмотрим условия его равновесия.

Для определения усилия спроецируем все силы, действующие на узел, на ось, перпендикулярную направлению стержня 1—3, т. е. на вертикальную ось у.

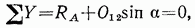
откуда

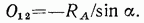
В данном случае RA равно а потому

Для определения усилия спроецируем все силы, действующие на опорный узел, на ось, перпендикулярную направлению стержня 1—2, т. е. на ось

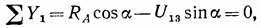
откуда

Отметим, что усилие в стержне 1—3 можно было определить и из уравнения проекций всех сил на ось х:

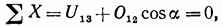
откуда

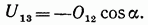
Подставив в последнее уравнение значение усилия полученное ранее, найдем

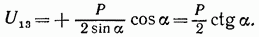
Для определения усилий в стержнях 3—2 и 3—5 вырежем узел 3 и рассмотрим условия его равновесия (рис. 4.24).

Составим сумму проекций сил на ось

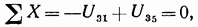
откуда (учитывая, что через обозначено одно и то же усилие, а именно усилие в стержне, соединяющем узлы 1—3), получим

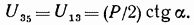
Спроецировав все силы на вертикальную ось у, получим

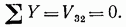
Усилие в стержне 3—2 было бы также равно нулю, если этот стержень и не был бы перпендикулярен стержням 1—3 и 3—5.

Рис. 4.24

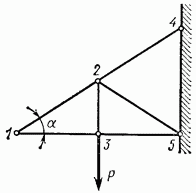
Рис. 4.25

Рис. 4.26

Следовательно, если в узле сходятся три стержня, два из которых лежат на одной прямой, то усилия в этих двух стержнях, при отсутствии в узле внешней нагрузки, равны друг другу по числовой величине и по знаку, а усилие в третьем стержне равно нулю.

Рассмотрим условия равновесия узла 2, найдем усилия в стержнях 2—4 и 2—5; они будут определяться через уже известные нам усилия (или и 1/32).

Таким образом, при расчете фермы способом вырезания узлов усилия в ряде стержней можно найти только после предварительного определения усилий в других стержнях. В связи с этим случайная ошибка в определении одного усилия может привести к неправильному определению усилий в целом ряде стержней. Кроме того, недостатком этого способа является и то, что в уравнения равновесия всегда входят тригонометрические функции; это усложняет расчет.

Отметим, что если к узлу, в котором сходятся два стержня, не лежащие на одной прямой, не приложена внешняя нагрузка, то усилия в этих стержнях равны нулю. В этом можно убедиться, рассмотрев условия равновесия узла 1 фермы, изображенной на рис. 4.25.

В самом деле, из уравнений проекций на вертикальную ось у и горизонтальную ось х всех сил, действующих на узел 1 (рис. 4.26),

следует, что

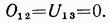
Обычно при расчете фермы пользуются и способом моментной точки и способом проекций, применяя каждый раз тот из них, с помощью которого более просто определяется усилие в данном элементе.

Пример 1. Определить усилия в элементах 4—6, 3—6 и 8—7 фермы-консоли, изображенной на рис. 4.27.

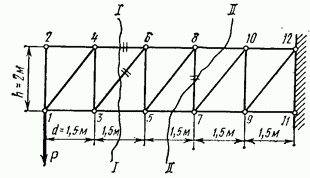
Рис. 4.27

Для определения усилий рассекаем ферму, как показано на рис. 4.27, и рассматриваем равновесие левых отсеченных частей. Расчет сведен в табл. 4.1.

Пример 2. Для ферм, изображенных на рис. 4.28, 4.29, 4.30 и 4.31, имеющих одинаковые пролеты и нагрузку, определить усилия во всех элементах (стержнях) и построить эпюры этих усилий.

Результаты расчета приведены соответственно на рис. 4.32, 4.33, 4.34 и 4.35 в виде эпюр усилий. Ширина каждой полоски этих эпюр пропорциональна числовой

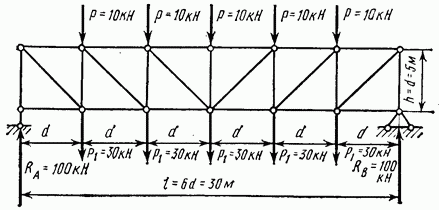
Рис. 4.28

Таблица 4.1. (см. скан)

величине усилия в соответствующем элементе фермы; полоски, изображающие положительные усилия (растяжение), не заштрихованы, а отрицательные (сжатие) — заштрихованы

Для фермы, изображенной на рис. 4.30, составлена табл. 4.2., в которую сведен весь расчет.

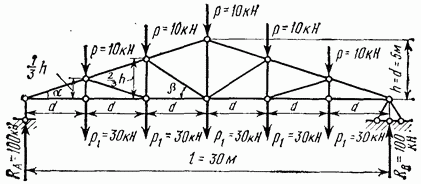
Рис. 4.29

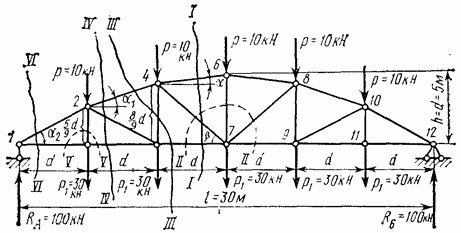
Рис. 4.30

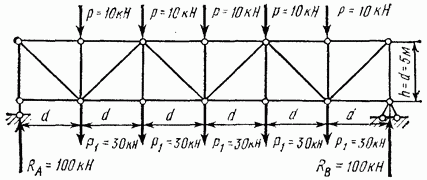
Рис. 4.31

Сравнивая между собой эпюры усилий в элементах трех ферм (имеющих одинаковые пролеты, один и тот же тип решетки, а также одинаковую нагрузку), представленные на рис. 4.32, 4.33 и 4.34, приходим к следующему заключению: самой невыгодной является треугольная ферма (см. рис. 4.29), так как общая площадь

полосок эпюры у нее больше, чем у каждой из двух других, и, следовательно, она окажется по массе наиболее тяжелой из трех рассматриваемых ферм.

Пример 3. Определить усилия в элементах фермы с параллельными поясами при полураскосной решетке (рис. 4.36, а).

Рис. 4.32

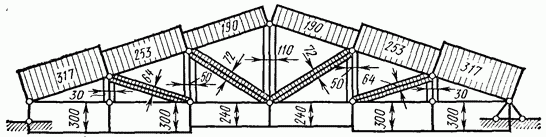
Рис. 4.33

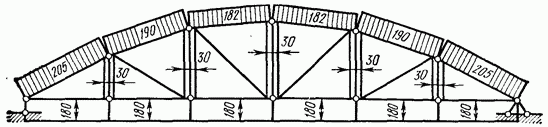
Рис. 4.34

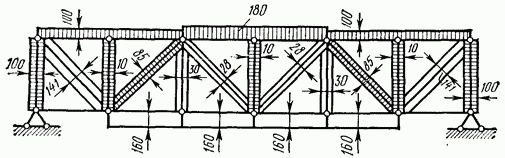
Рис. 4.35

Вырежем любой средний узел (где два полураскоса одной панели пересекаются со стойкой) и спроецируем все действующие на него усилия на горизонтальную ось (рис. 4.36, б):

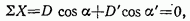
откуда