Вычислений перемещений методом Мора

Излагаемый ниже метод является универсальным методом определения перемещений (как линейных так и угловых), возникающих в любой стержневой системе от произвольной нагрузки.

Рассмотрим два состояния системы. Пусть в первом из них (грузовое состояние) к балке приложена любая произвольная нагрузка, а во втором (единичное состояние) – сосредоточенная сила (рис.25).

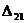Работа А21 силы на перемещении , возникающем от сил первого состояния:

.

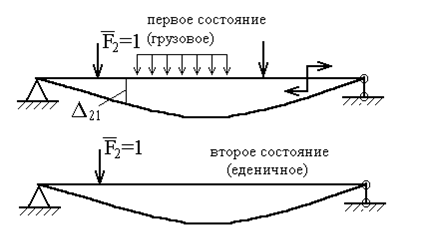
Рис.25

Используя (2.14) и (2.15), выразим А21 (а, значит, и 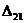) через внутренние силовые факторы:

(2.17)

Знак “+”, полученный при определении 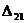, означает, что направление искомого перемещения совпадает с направлением единичной силы. Если определяется линейное смещение, то обобщенная единичная сила представляет собой безразмерную сосредоточенную единичную силу, приложенную в рассматриваемой точке; а если определяется угол поворота сечения, то обобщенная единичная сила – это безразмерный сосредоточенный единичный момент.

Иногда (2.17) записывается в виде:

(2.18)

где 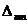- перемещение по направлению силы , вызванное действием группы сил 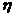. Произведения, стоящие в знаменателе формулы (2.18), называются соответственно жесткостями при изгибе, растяжении (сжатии) и сдвиге; при постоянных по длине размерах сечения и одинаковом материале эти величины можно выносить за знак интеграла. Выражения (2.17) и (2.18) называются интегралами (или формулами) Мора.

Наиболее общий вид интеграл Мора имеет в том случае, когда в поперечных сечениях стержней системы возникают все шесть внутренних силовых факторов:

(2.19)

Алгоритм вычисления перемещения методом Мора состоит в следующем:

1. Определяют выражения внутренних усилий от заданной нагрузки как функций координаты Z произвольного сечения.

2. По направлению искомого перемещения прикладывается обобщенная единичная сила (сосредоточенная сила – при вычислении линейного перемещения; сосредоточенный момент – при вычислении угла поворота).

3. Определяют выражения внутренних усилий от обобщенной единичной силы как функций координаты Z произвольного сечения.

4. Подставляют выражение внутренних усилий, найденные в п.п.1, 3 в (2.18) или (2.19) и интегрированием по участкам в пределах всей длины конструкции определяют искомое перемещение.

Формулы Мора пригодны и для элементов, представляющих собой стержни малой кривизны, с заменой элемента длины dz в подынтегральном выражении элементом дуги ds.

В большинстве случаев плоской задачи используется только один член формулы (2.18). Так, если рассматриваются конструкции, работающие преимущественно на изгиб (балки, рамы, а частично и арки), то в формуле перемещений с соблюдением достаточной точности можно оставить только интеграл, зависящий от изгибающих моментов; при расчете конструкций, элементы которых работают, в основном, на центральное растяжение (сжатие), например, ферм, можно не учитывать деформации изгиба и сдвига, то есть в формуле перемещений останется только член, содержащий продольные силы.
Аналогично, в большинстве случаев пространственной задачи существенно упрощается формула Мора (2.19). Так, когда элементы системы работают преимущественно на изгиб и кручение (например, при расчете плоско-пространственных систем, ломаных стержней и пространственных рам) в (2.19) остаются только первые три члена; а при расчете пространственных ферм – только четвертый член.