Перемещения статически определимых систем, вызываемые перемещениями опор

При перемещениях опор статически определимого сооружения по направлениям опорных закреплений внутренние усилия в сооружении не возникают.

В качестве примера рассмотрим раму, изображенную на рис. 5.31, а. Предположим, что в результате размыва грунта под фундаментом или по какой-либо другой причине шарнирно подвижная опора рамы, схематически изображенная вертикальным стержнем В, переместилась по вертикали, т. е. по направлению опорного

стержня, на величину А. Такое смещение опоры не вызовет в сооружении внутренних усилий.

Определим перемещение точки k системы по направлению i — i, т. е. перемещение . Для этого создадим единичное состояние данной системы и в направлении искомого перемещения приложим к ней силу (рис. 5.31, б). Опорную реакцию, возникающую (в единичном состоянии) от силы в том опорном стержне, который в действительном состоянии сооружения перемещается на величину А, обозначим

Рис. 5.31

На основании теоремы о взаимности работ для двух состояний, изображенных на рис. 5.31, а, б, в одном из которых (в действительном) сооружение не загружено (т. е. как бы находится под действием нулевой нагрузки), можно составить следующее уравнение:

или

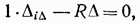
откуда

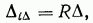
т. е. перемещение 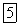какой-либо точки заданного статически определимого сооружения, возникающее от линейного смещения опоры на величину , равно произведению смещения на реакцию связи (которая в действительном состоянии смещается на величину ) от действия единичной нагрузки, приложенной в направлении искомого перемещения. Это перемещение положительно, когда реакция связи направлена обратно смещению , и отрицательно, когда она совпадает с ним.

Тот же результат можно получить, если составить следующее равенство работ:

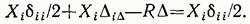
Левая часть этого уравнения представляет собой работу всех сил, в том числе и опорных реакций, приложенных к заданной статически определимой системе (рис. 5.32, а), которую они совершат в случае, если перемещение опоры В начнется после того, как

закончится статическое нарастание силы . Правая же часть уравнения представляет собой работу тех же сил в случае, если сначала произойдет смещение опоры В и лишь после этого на систему начнет действовать статически нарастающая сила (рис. 5.32, б).

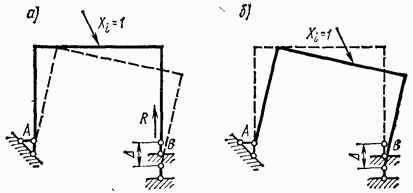
Рис. 5.32

Левая часть уравнения равна правой потому, что окончательная деформация системы в обоих случаях будет одна и та же; это позволяет утверждать, что потенциальная энергия, накопленная в системе в первом случае (равная сумме слагаемых левой части уравнения), будет равна потенциальной энергии (равной правой части уравнения), накопленной во втором случае.

Из полученного уравнения следует (учитываем, что ):

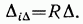
Этот же результат был получен нами выше на основании теоремы о взаимности работ.

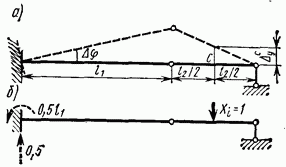
Рис. 5.33

Рассмотрим теперь шарнирную балку, показанную на рис. 5.33, а, левая опора которой (заделка) повернулась на угол . При этом левый конец балки также повернулся на угол . Определим вертикальное перемещение Д? точки С балки. Для этого создадим единичное состояние балки и в направлении искомого перемещения приложим к ней силу (рис. 5.33, б). На основании теоремы о взаимности работ для двух состояний, изображенных на рис. 5.33, можно составить уравнение

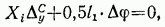
или

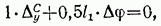
откуда

Знак минус указывает на то, что точка С переместилась в сторону, противоположную направлению силы т. е. вверх.

Рассмотрим теперь общий случай, когда одновременно происходят перемещения в направлениях нескольких опорных закреплений статически определимого сооружения. В качестве конкретного примера рассмотрим систему, изображенную на рис. 5.34, а. Штриховой линией показано новое положение системы, вызванное смещением правой опоры по вертикали и горизонтали соответственно на а и b.

Рис. 5.34

Определим угол поворота узла Е заданной системы. Для этого, решая задачу с помощью теоремы о взаимности работ, создадим единичное состояние системы (рис. 5.34, б), приложив к ней в направлении искомого углового перемещения единичный момент . Под влиянием этого момента на правой опоре возникнут реакции и соответственно равные 1/l и 1/(2h).

Составим следующее равенство работ для двух состояний системы — действительного (рис. 5.34, а) и единичного (рис. 5.34, б):

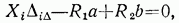
откуда (так как )

Подставив значения реакций получим

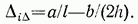
Итак, для определения перемещения, возникающего в статически определимом сооружении от смещения его опор (в направлениях опорных закреплений), необходимо:

1) выбрать единичное состояние сооружения, считая смещающуюся связь неподвижной;

2) загрузить сооружение (в единичном состоянии) в направлении искомого перемещения силой или моментом

3) определить реакции в тех опорных связях единичного состояния, которые в действительном состоянии сооружения смещаются;

4) составить выражение работы сил единичного состояния на перемещениях действительного и приравнять его нулю;

5) решить полученное уравнение относительно искомого перемещения.