Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Определение невыгоднейшего положения нагрузки на сооружении. Эквивалентная нагрузка
|
|
В предыдущем параграфе было доказано, каким образом с помощью линии влияния определяются различные усилия (например, опорная реакция, изгибающий момент, поперечная сила и т. д.) от нагрузки, расположение которой задано. Теперь покажем, как надо расположить заданную нагрузку на сооружении, чтобы она вызвала наибольшее значение рассматриваемого усилия. Такое положение нагрузки называется невыгоднейшим или опасным.
1. Случай действия на сооружение подвижной равномерно распределенной нагрузки. В § 2.5 было показано, что числовая величина усилия S от равномерно распределенной нагрузки равна произведению интенсивности нагрузки q на площадь линии влияния, измеренную в пределах расположения нагрузки, т. е.  Так как интенсивность нагрузки q есть величина постоянная, то максимальное значение искомого усилия получится при наибольшем значении
Так как интенсивность нагрузки q есть величина постоянная, то максимальное значение искомого усилия получится при наибольшем значении
площади  а это будет в том случае, когда нагрузка q расположится над всей площадью линии влияния одного знака.
а это будет в том случае, когда нагрузка q расположится над всей площадью линии влияния одного знака.
На рис. 2.21, а показано загружение равномерно распределенной нагрузкой, соответствующее шах 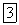 (загружена вся положительная часть линии влияния
(загружена вся положительная часть линии влияния  , а на рис. 2.21, б, - соответствующее
, а на рис. 2.21, б, - соответствующее 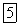 (загружена вся отрицательная часть линии влияния). На рис. 2.22, а, показано загружение, соответствующее
(загружена вся отрицательная часть линии влияния). На рис. 2.22, а, показано загружение, соответствующее  (загружены оба положительных участка линии влияния).
(загружены оба положительных участка линии влияния).
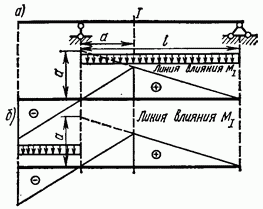
Рис. 2.21

Рис. 2.22
Наконец, на рис. 2.22, б показано загружение, соответствующее  (загружена вся отрицательная часть линии влияния).
(загружена вся отрицательная часть линии влияния).
2. Случай действия системы жестко связанных сосредоточенных сил 2. Система жестко связанных подвижных сосредоточенных сил моделирует действие движущегося экипажа или поезда.
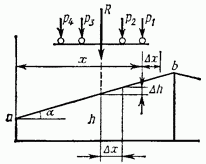
Рис. 2.23
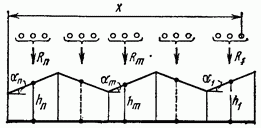
Рис. 2.24
Если все грузы находятся над прямолинейным участком линии влияния, то, как следует из предыдущего параграфа, их действие можно заменить равнодействующей (см. рис. 2.20). Рассмотрим систему жестко связанных
связанных грузов, изображенных на рис. 2.23, положение которых будем характеризовать координатой х (расстояние от начала линии влияния до первого груза). Допустим, что система грузов переместилась на  при этом ни один из грузов не сошел с участка а — b. Очевидно, что при таком перемещении равнодействующая тоже переместится на
при этом ни один из грузов не сошел с участка а — b. Очевидно, что при таком перемещении равнодействующая тоже переместится на  и ордината под ней изменится на
и ордината под ней изменится на 

Значит, усилие S получит приращение
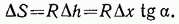
В общем случае, когда загружено несколько участков линии влияния, нельзя заменить всю нагрузку равнодействующей, но можно сделать это на каждом участке (рис. 2.24), тогда
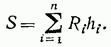
Если нагрузка переместится на небольшое расстояние  так, что все грузы останутся на тех же участках, то равнодействующие на всех участках не изменятся, а усилие S получит приращение
так, что все грузы останутся на тех же участках, то равнодействующие на всех участках не изменятся, а усилие S получит приращение

откуда
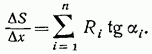
В соответствии с выражением (2.6) приращение усилия линейно зависит от  пока ни один из грузов не перейдет через вершину
пока ни один из грузов не перейдет через вершину  следовательно, график изменения усилия в зависимости от
следовательно, график изменения усилия в зависимости от  будет линейным. Причем, перелом возникает в том случае, когда один из грузов переходит через вершину линии влияния. На рис. 2.25 изображен график зависимости усилия S от положения грузов, характеризуемого координатой
будет линейным. Причем, перелом возникает в том случае, когда один из грузов переходит через вершину линии влияния. На рис. 2.25 изображен график зависимости усилия S от положения грузов, характеризуемого координатой  (см. рис. 2.24). В соответствии с рис. 2.25 и выражением (2.7) имеем
(см. рис. 2.24). В соответствии с рис. 2.25 и выражением (2.7) имеем
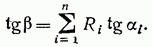

Рис. 2.25
Критерием достижения  будет изменение знака выражения
будет изменение знака выражения  при переезде грузов через одну из вершин линии влияния либо обращение в нуль этой суммы, что соответствует горизонтальной
при переезде грузов через одну из вершин линии влияния либо обращение в нуль этой суммы, что соответствует горизонтальной
линии на графике в верхней части рис. 2.25. Обратим внимание на то, что этот критерий не является корректным, если график имеет несколько максимумов. Критерий позволяет определить только локальный (местный) максимум, но практически этого бывает достаточно. При вычислении вручную трудно перебрать все возможные положения груза над вершинами. В каждом конкретном случае положение, близкое к невыгодному, можно установить по смыслу и далее исследовать небольшое число положений грузов над вершинами, найдя при каком из них величина  изменяет знак.
изменяет знак.
Наиболее часто встречающимся случаем является загружение треугольной линии влияния (рис. 2.26), когда задача решается проще. Сумма (2.8) записывается в виде

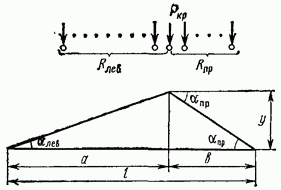
Рис. 2.26
Ее знак не зависит от величины у и задача нахождения опасного загружения сводится к определению того груза, переход которого через вершину линии влияния изменяет знак величины  Этот груз называется критическим. Задачу нахождения груза
Этот груз называется критическим. Задачу нахождения груза  можно сформулировать по-другому. Допустим, этот груз найден, тогда можно мысленно его «расщепить» на две части, включив одну часть
можно сформулировать по-другому. Допустим, этот груз найден, тогда можно мысленно его «расщепить» на две части, включив одну часть  другую — в
другую — в  так, что разность
так, что разность  обратится в нуль. В этом случае
обратится в нуль. В этом случае  Задача нахождения невыгодного загружения упростилась до определения такого положения нагрузки, при котором она делится в заданном отношении. Итак,
Задача нахождения невыгодного загружения упростилась до определения такого положения нагрузки, при котором она делится в заданном отношении. Итак,

где  - полная равнодействующая.
- полная равнодействующая.
Решая систему (2.9), получим
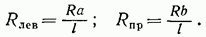
Формулы (2.10) могут быть использованы только в том случае, когда поезд полностью располагается над треугольной линией влияния. Поскольку невыгодное положение нагрузки не зависит от размера ординаты у, можно для каждого вида подвижной нагрузки, а также различных I и  найти
найти  при
при  Далее можно действие подвижной нагрузки при невыгодном ее расположении заменить действием нагрузки, равномерно распределенной по всей
Далее можно действие подвижной нагрузки при невыгодном ее расположении заменить действием нагрузки, равномерно распределенной по всей
длине l. Она называется эквивалентной нагрузкой. Ее интенсивность  находится приравниванием
находится приравниванием  и результата загружения треугольника равномерно распределенной нагрузкой:
и результата загружения треугольника равномерно распределенной нагрузкой:
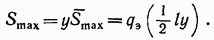
Откуда
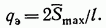
Эквивалентная нагрузка зависит от длины треугольной линии влияния  положения ее вершины
положения ее вершины  и типа подвижной нагрузки. Имеются готовые таблицы эквивалентных нагрузок для различных типов электровозов, тепловозов, вагонов и т. д. при
и типа подвижной нагрузки. Имеются готовые таблицы эквивалентных нагрузок для различных типов электровозов, тепловозов, вагонов и т. д. при  которые приведены в соответствующих нормативных документах, например, в «Указаниях по определению условий пропуска поездов по железнодорожным мостам».
которые приведены в соответствующих нормативных документах, например, в «Указаниях по определению условий пропуска поездов по железнодорожным мостам».
При выполнении конкретного расчета инженер-проектировщик пользуется табличными значениями  Максимально возможное усилие вычисляется через площадь линии влияния
Максимально возможное усилие вычисляется через площадь линии влияния  по формуле
по формуле

Пример. На рис. 2.27, а показана схема сплотки (двух секций) электровозов  Расстояние между осями указаны в
Расстояние между осями указаны в  а силы (давление на оси) в
а силы (давление на оси) в  На рис. 2.27, б показана треугольная линия влияния. Требуется определить невыгодное расположение сплотки электровозов и эквивалентную нагрузку.
На рис. 2.27, б показана треугольная линия влияния. Требуется определить невыгодное расположение сплотки электровозов и эквивалентную нагрузку.
Решение. Вычислим равнодействующую 
По формуле (2.10) определим 

Вычислим отношение, указывающее, сколько грузов входит в 
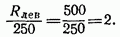
Принимаем в качестве критического 7-й груз (см. рис. 2.27, а, б) и относим его целиком к  . Вычислим
. Вычислим  :
:

Для определения ординат линии влияния под грузами иайдем расстояния от грузов до начала и конца линии влияния (рис. 2.27, а). Далее вычисляем 
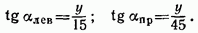
В соответствии с рис. 2.27, а и формулой (2.11) имеем
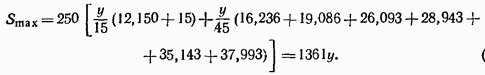 (2.12)
(2.12)
С другой стороны,
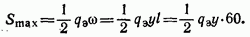
Приравнивая выражения (2.12), (2.13) и сокращая на у, получим
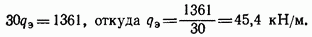
Можно для определения  использовать формулу (2.10):
использовать формулу (2.10):
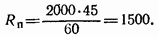

Рис. 2.27
Вычисляем отношение  принимаем в качестве критического
принимаем в качестве критического  и
и
6-й груз (рис. 2.27, в) и включаем его в равнодействующую правых сил  Аналогично предыдущему, вычислим
Аналогично предыдущему, вычислим