Температурные перемещения

Формула Мора (5.22) -(5.24) может быть представлена в виде

где - взаимный угол поворота торцовых сечений элемента стержня от заданной нагрузки; 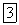- взаимное смещение их в направлении оси стержня; взаимное смещение их в направлении нормали к оси стержня (см. § 5.1).

В таком виде формула Мора может быть использована, когда деформации элемента стержня вызваны не только внутренними усилиями в его поперечных сечениях от нагрузки, но и действием температуры на сооружение. Следовательно, формулой Мора в приведенном виде можно пользоваться и для определения перемещений системы, вызванных действием температуры.

Рис. 5.28

Пусть верхнее волокно элемента dx нагрето на а нижнее — на (рис. 5.28).

Распределение температуры по высоте поперечного сечения примем по прямолинейному закону.

При температурном коэффициенте линейного расширения а удлинение верхнего волокна равно , а удлинение нижнего волокна составляет Осевое удлинение можно получить как среднее арифметическое указанных величин (при поперечном сечении, симметричном относительно горизонтальной оси):

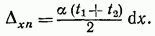
Угол взаимного поворота крайних поперечных сечений (элемента dx) равен:

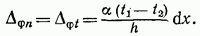
Деформации сдвига в элементе от действия температуры не возникают, т. е. .

Подставив найденные значения в выражение (5.29), получим формулу для отыскания температурных перемещений:

Знаки означают суммирование по всем стержням и участкам сооружения.

При вычислении перемещения интегрирование распространяется лишь на те элементы сооружения, температурный режим

которых изменился. Для случая прямолинейных или ломаных стержней постоянного сечения интегралы могут быть подсчитаны как площади единичных эпюр, и формула перемещений принимает простой вид:

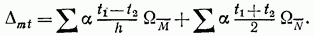
Здесь — площади единичных эпюр М и

При поперечном сечении элемента, несимметричном относительно горизонтальной оси, в формулы вместо входит выражение , где у — расстояние от нижнего волокна элемента до горизонтальной оси, проходящей через центр тяжести поперечного сечения.

Знаки членов формулы определяют так: если деформации элемента от температуры и от единичной силы аналогичны, то знак соответствующего члена будет положительным, и наоборот.

При определении перемещений от действия на сооружение температуры нельзя пренебрегать членом формулы, зависящим от продольной силы.

Пример. Для ломаного бруса, изображенного на рис. 5.29, а, отыскать вертикальное перемещение точки С, если температура снаружи не изменилась, а внутри повысилась на 10°С (рис. 5.29, а).

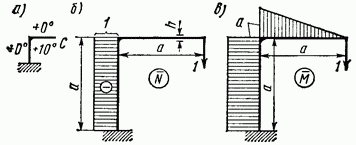
Рис. 5.29

Решение. По направлению искомого перемещения прикладываем единичную силу и строим от нее эпюры N и М (рис. 5.29, б, в).

Подсчитаем площади единичных эпюр:

Найдем температурные сомножители:

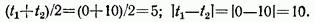
Последняя запись указывает на то, что разность температур берется по абсолютной величину.

Температурное воздействие вызывает удлинение внутренних волокон бруса, а единичная сила — их укорочение; поэтому у члена формулы температурных перемещений, учитывающего изгибающие моменты, следует поставить знак минус. Знак минус надо поставить и перед членом с продольной силой, так как изменение температуры вызывает удлинение стойки, а действие единичной силы — укорочение стойки. Таким образом,