
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Теорема о взаимности возможных работ
|
|
Рассмотрим два состояния какого-либо сооружения, например балки на двух опорах (рис. 6.10, а). В состоянии i на эту балку действует обобщённая сила Fi, а состоянии j – обобщённая сила Fj. Обобщённые силы Fi и Fj в упомянутых состояниях прикладываются статическим способом. На рис. 6.10, а показаны действительные (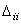 ,
, 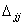 ) и возможные (
) и возможные ( ,
, 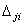 ) перемещения по направлению обобщённых сил.
) перемещения по направлению обобщённых сил.
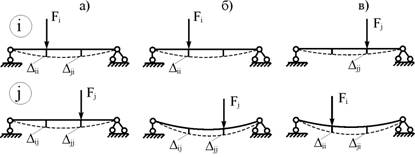
Рис.6.10
Вычислим работу обобщённых сил Fi и Fj от их совместного воздействия. Сначала статическим способом приложим обобщённую силу Fi, которая на перемещении 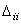 будет совершать действительную работу Wext, ii(рис. 6.10, б). После окончательного формирования обобщённой силы Fi статическим способом приложим обобщённую силу Fj. Балка получит дополнительные деформации и перемещения:
будет совершать действительную работу Wext, ii(рис. 6.10, б). После окончательного формирования обобщённой силы Fi статическим способом приложим обобщённую силу Fj. Балка получит дополнительные деформации и перемещения:  – возможное перемещение в направлении обобщённой силы Fi от действия обобщённой силы Fj,
– возможное перемещение в направлении обобщённой силы Fi от действия обобщённой силы Fj, 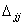 – действительное перемещение в направлении обобщённой силы Fj от её же воздействия (рис. 6.10, б внизу). Постоянная по величине обобщённая сила Fiсовершает возможную работу Wext, ij на перемещении
– действительное перемещение в направлении обобщённой силы Fj от её же воздействия (рис. 6.10, б внизу). Постоянная по величине обобщённая сила Fiсовершает возможную работу Wext, ij на перемещении  , а статически приложенная сила Fj – действительную работу Wext, jj на перемещении
, а статически приложенная сила Fj – действительную работу Wext, jj на перемещении 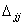 . Суммарная работа
. Суммарная работа 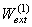 внешних обобщённых сил будет равна
внешних обобщённых сил будет равна
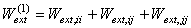 .
.
Зависимости для вычисления действительной и возможной работы внешних обобщённых сил Fi и Fj:
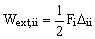 ,
,
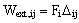 ,
,
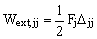 .
.
Таким образом, выражение суммарной работы от совместного действия обобщённых сил Fi и Fj в случае, когда первой прикладывается сила Fi, а второй Fj, примет вид:
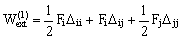 . (6.1)
. (6.1)
Рассмотрим обратный порядок приложения обобщённых сил: первой приложим статическим способом обобщённую силу Fj, а затем, после её окончательного формирования, – обобщённую силу Fi (рис. 6.10, в). Суммарная работа внешних обобщённых сил Fi и Fj 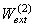 в этом случае запишется:
в этом случае запишется:
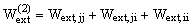 .
.
Учитывая, что 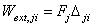 , получим:
, получим:
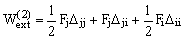 . (6.2)
. (6.2)
Значение суммарной работы внешних обобщённых сил Fi и Fj не зависит от последовательности их приложения, т.е.
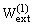 =
= 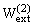 .
.
Приняв во внимание соотношения (6.1) и (6.2) окончательно будем иметь:
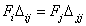 , или
, или
Wext, ij = Wext, ji. (6.3)
Выражение (6.3) и составляет содержание теоремы о взаимности возможных работ внешних сил: возможная работа i-й обобщённой силы (внешних сил i-го состояния) на перемещениях, вызванных j-й обобщённой силой (внешними силами j-го состояния), равна возможной работе j-й обобщённой силы (внешних сил j-го состояния) на перемещениях, вызванных i-й обобщённой силой (внешними силами i-го состояния). В строительной механике эта теорема носит имя итальянского учёного Энрико Бетти (1823–1892).
Без доказательства отметим справедливость теоремы Бетти для внутренних сил
Wint, ij = Wint, ji,
т.е. возможная работа внутренних сил i-го состояния на деформациях j-го состояния равна возможной работе внутренних сил j-го состояния на деформациях i-го состояния.
Из теоремы Бетти, как частный случай, вытекают другие теоремы взаимности строительной механики, широко используемые в расчётах сооружений.
6.2.2. Теорема о взаимности перемещений
По-прежнему рассмотрим состояния i и j одного и того же сооружения (рис. 6.11). В состоянии i на него действует сила Fi = 1, а в состоянии j – сила Fj = 1. Зафиксируем возможные перемещения 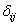 и
и 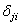 , возникающие в состояниях i и j от единичных сил.
, возникающие в состояниях i и j от единичных сил.
Для состояний сооружения i и j применим теорему о взаимности возможных работ внешних сил (см. соотношение (6.3)):
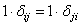 , или
, или 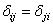 . (6.4)
. (6.4)
Соотношение (6.4) выражает содержание теоремы о взаимности перемещений: перемещение по направлению линии действия i-й единичной обобщённой силы, вызванное j-й единичной обобщённой силой, равно перемещению по направлению линии действия j-й обобщённой силы от i-й единичной обобщённой силы. В строительной механике эта теорема известна как теорема английского физика и механика Джеймса Максвелла (1831–1879).
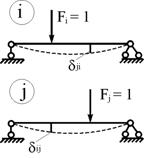
Рис.6.11
Теорема о взаимности перемещений широко применяется в расчётах линейно деформируемых систем, в частности, в расчётах статически неопределимых систем методом сил, при построении линий влияния перемещений в стержневых сооружениях.
Выше был рассмотрен случай, когда в состоянии i и j сооружения действуют единичные сосредоточенные силы (рис. 6.11), т.е. силы, имеющие одинаковую природу и одинаковую размерность. На рис. 6.12 рассмотрена ситуация, когда в состоянии i на сооружение действует сосредоточенная сила Fi = 1, а состоянии j – сосредоточенный момент Mj = 1. Здесь же показаны и возможные перемещения 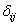 и
и 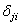 , вызываемые упомянутыми силами Fi = 1 иMj = 1. Кажущееся противоречие в размерностях перемещений
, вызываемые упомянутыми силами Fi = 1 иMj = 1. Кажущееся противоречие в размерностях перемещений 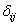 и
и 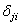 , равенство которых определено соотношением (6.4), отпадает, если мы примем во внимание, что каждое из этих перемещений является удельным перемещением, т.е. что оно вызывается обобщённой силой, имеющей не произвольное, а единичное значение. Таким образом, размерность какого-либо удельного перемещения есть отношение размерности рассматриваемого обобщённого перемещения к размерности обобщённой силы, вызвавшей это перемещение. В случае, рассмотренном на рис. 6.12, имеем:
, равенство которых определено соотношением (6.4), отпадает, если мы примем во внимание, что каждое из этих перемещений является удельным перемещением, т.е. что оно вызывается обобщённой силой, имеющей не произвольное, а единичное значение. Таким образом, размерность какого-либо удельного перемещения есть отношение размерности рассматриваемого обобщённого перемещения к размерности обобщённой силы, вызвавшей это перемещение. В случае, рассмотренном на рис. 6.12, имеем:
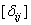 = см/кНсм = кН-1,
= см/кНсм = кН-1, 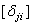 = рад/кН = кН-1,
= рад/кН = кН-1,
т.е. оба перемещения имеют одинаковую размерность.
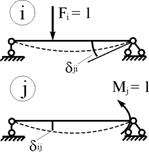
Рис.6.12
19Определение перемещений в стержневых системах
наиболее общим методом определения перемещений в стержневых системах является метод Мора (иногда говорят: Максвелла – Мора), в основе которого лежат два основных принципа механики: начало возможных перемещений и закон сохранения энергии. Прежде чем перейти к изложению метода, остановимся на его основных теоретических предпосылках.