
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Метод интегрирования по частям. Формулой интегрирования по частям в неопределенном интеграле называется формула
|
|
Формулой интегрирования по частям в неопределенном интеграле называется формула
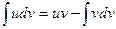
где u=u(x) и v=v(x) дифференцируемые функции от х. Она позволяет свести нахождение интеграла 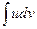 к нахождению интеграла
к нахождению интеграла 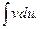
Большую часть интегралов, при нахождении которых применяется формула интегрирования по частям, можно разбить на три группы.
1. Интегралы вида
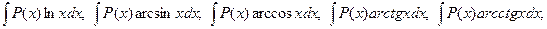
где Р(х) многочлен некоторой степени n. За функцию u(x) следует взять одну из функций 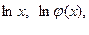
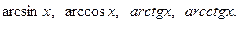 , тогда
, тогда 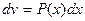 .
.
2. Интегралы вида
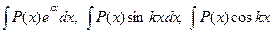 ,
,
где Р(х) многочлен, а k – некоторое число. Для их нахождения следует положить u=P(x), а 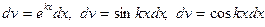 соответственно.
соответственно.
3. Интегралы вида
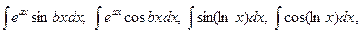
где a и b – некоторые числа. Эти интегралы находятся с помощью двукратного интегрирования по частям.
Пример. Найти интеграл 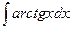 Решение. Применим формулу интегрирования по частям. За функцию u(x) возьмем
Решение. Применим формулу интегрирования по частям. За функцию u(x) возьмем 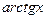 , тогда
, тогда 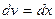 . Будем иметь
. Будем иметь
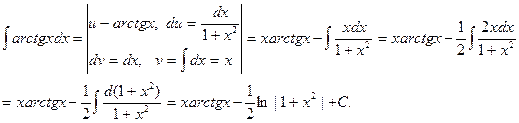
Пример. Найти интеграл 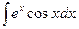
Решение. 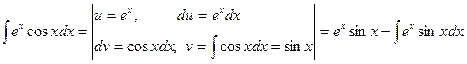
Полученный интеграл снова находим интегрированием по частям.
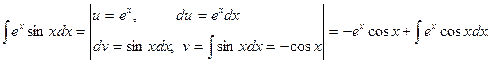
Подставляя значение полученного интеграла в предыдущее выражение, будем иметь
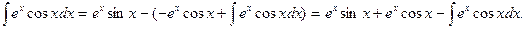
Перенося искомый интеграл из правой части равенства в левую, получаем
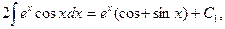
Окончательно имеем
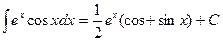 .
.