Интегрирование выражений, содержащих тригонометрические функции

1) Интеграл 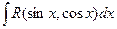. Функция R(sinx, cosx) есть рациональная функция относительно sinx, cosx. Тогда интеграл 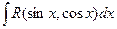рационализируется с помощью универсальной тригонометрической подстановки

=

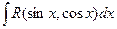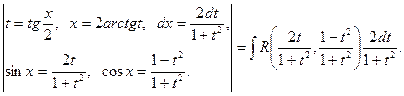
Универсальная тригонометрическая подстановка приводит часто к сложным рациональным функциям. Поэтому в ряде случаев более удобны другие подстановки:

а) функция R(sinx.cosx) есть нечетная функция относительно sinx.

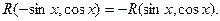Применяется подстановка t=cosx.

б) функция R(sinx.cosx) есть нечетная функция относительно cosx.

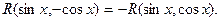Применяется подстановка t=sinx

в) функция R(sinx.cosx) есть четная функция относительно sinx и cosx.

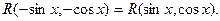Применяется подстановка t=tgx.

2) Интегралы вида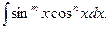

а) Если хотя бы одно из чисел m или n –положительное нечетное число, то, отделяя от нечетной степени один сомножитель и выражая с помощью формулы 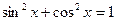оставшуюся четную степень через дополнительную функцию, приходим к табличному интегралу.

Пример. Найти интеграл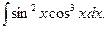

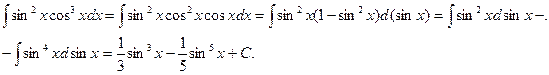
б) Если же m и n четные неотрицательные числа, то степени понижаются с помощью тригонометрических формул:

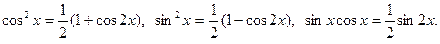
Пример. Найти интеграл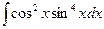

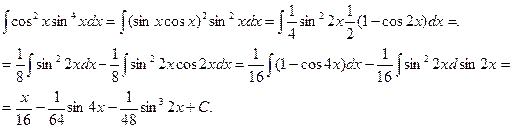
3) Интегралы вида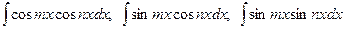

преобразуются к табличным интегралам с помощью формул

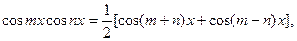
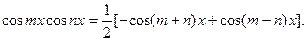
Примеры. Найти интегралы:

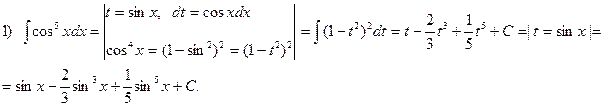
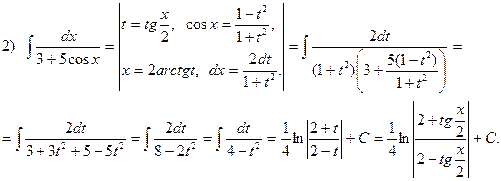
3)