Несобственные интегралы с бесконечными пределами интегрирования

Пусть функция y=f(x) определена и непрерывна при всех значениях х на бесконечном интервале 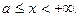Для любого конечного сегмента [ a, b ] интеграл 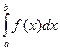существует и является непрерывной функцией от х.

Если существует конечный предел

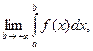
то этот предел называют несобственным интегралом от функции f(x) на интервале 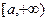и обозначают символом .

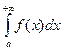По определению имеем

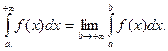
В этом случае говорят, что несобственный интеграл 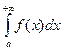существуетилисходится. Если указанный предел не существует или бесконечен, то говорят, что интеграл ву не существует или расходится.

Аналогично определяются несобственные интегралы:

.

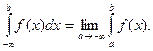
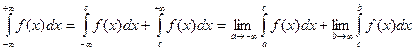где с – любая фиксированная точка оси Ох.

Из определений ясно, что несобственный интеграл является не пределом интегральных сумм, а пределом определенного интеграла с переменной границей интегрирования.

Если f(x) ³ " х Î [ а; +¥), то несобственный интеграл 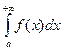можно рассматривать как площадь бесконечной криволинейной трапеции, ограниченной кривой y=f(x), бесконечным интервалом оси Ох [ a, +¥) и прямой х = а.

Пример. Исследовать сходимость несобственного интеграла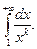

Решение. Рассмотрим интеграл .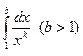

Если k¹ 1, то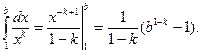

Если же k= 1, то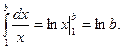

При k > 1, 1- k < 0 и поэтому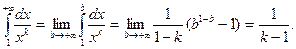

При k < 1, 1- k> 0 и поэтому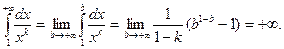

Если же k= 1, то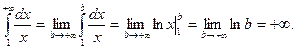

Таким образом, при 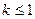интеграл расходится, при 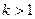интеграл сходится.