Интегрирование иррациональных и трансцендентных функций.

Предварительно введем понятие рациональной функции от двух переменных u и v, то есть функции получающейся из этих переменных и некоторых постоянных, над которыми производятся только операции сложения, вычитания, умножения и деления R (u, v). Такова, например, функция

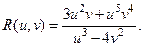
Если переменные u и v, в свою очередь являются функциями переменной x: 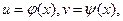то функция 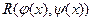называется рациональной функцией от 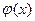и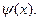

Рассмотрим теперь интегралы от некоторых простейших иррациональных и трансцендентных функций сводящихся к интегралам от рациональных функций.

1. Интегралы вида где a, b, c, d – некоторые числа 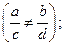m – натуральное число. Интегралы данного вида рационализируются подстановкой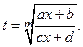

2. Интеграл вида где a, b, c – некоторые числа 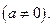Данный интеграл зависит от корней квадратного трехчлена 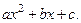Если этот трехчлен имеет два различных действительных корня x ₁ и x ₂, то он сводится к интегралу вида 1, а именно к интегралу

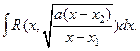
Если x ₁= x ₂, то интеграл сводится к интегралу от рациональной функции, а именно к интегралу

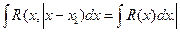
Если же квадратный трехчлен не имеет вещественных корней, то с помощью подстановки Эйлера

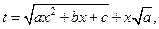
данный интеграл приводится к интегралу от рациональной функции

3. Интеграл вида 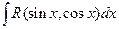рационализируется подстановкой 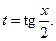Действительно,

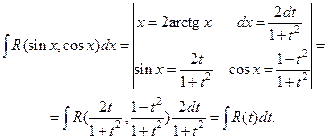
4. Интеграл вида 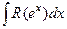рационализируется подстановкой 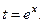Действительно,

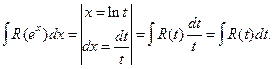
Практическое занятие 10