Таким образом, задание нормы на линейном пространстве преобразует его в нормированное пространство.

В любом нормированном пространстве А формула

r (x, y) = (10.1)

определяет метрику.

Действительно:

1) r (x, y) = ;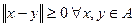

r (x, y) = 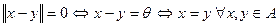Û x = y;

2) r(x, y) = 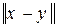= = = 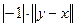r (y, x);

3) r (x, y) =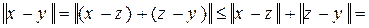

=r (x, z) + r (z, y).

Метрика r, которая введена по формуле (10.1), обладает двумя дополнительными свойствами:

4) r (x, y) = r (x + z, y + z);

5) r (lx, ly) = r (x, y).

Возникает вопрос о возможности введения нормы в линейном метрическом пространстве через метрику. Оказывается, что это возможно не всегда. Но имеет место следующее утверждение:

если в линейном метрическом пространстве А метрика r обладает двумя дополнительными свойствами 4–5, то функция r (х, q) является нормой на линейном пространстве А и эта норма порождает первоначальную метрику: = = 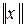r (х, q).

3Проверим выполнение аксиом нормы:

1) 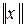= r (х, q) ³ 0, 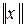= r (х, q)= 0 Û х = q;

2) =r (lx, q) =r (lx, l× q) = ê l ê × r (х, q) = ê l ê × ;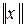

3) 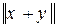= r (х + y, q) = r (х, -y) £ r (х, q) + r (-y, q) = 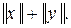4