
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Неопределенный интеграл.
|
|
Интегралы
Краткий курс лекций
Составитель Ю.В.Обрубов
Калуга - 2012
Неопределенный интеграл.
В дифференциальном исчислении основной задачей является нахождение производной дифференциала от данной функции.
В интегральном исчислении основной задачей является обратная задача – отыскание функции F(x) по заданной ее производной f(x) или дифференциалу f(x)dx, т.е. для данной функции f(x) надо найти такую функцию F(x), что:
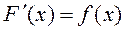 |
 |
или
Опр.
Функция F(x) называется первообразной для функции f(x) если на отрезке [a, b], если во всех точках этого отрезка выполняются равенства
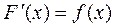 |
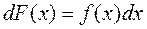 или
или
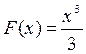
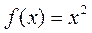 |
Например, для функции, то первообразная
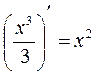
будет т.к.
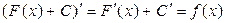 Легко видеть, что если F(x) первообразная функции для функции f(x), то функция (F(x)+C) тоже является первообразной для функции f(x), так как.
Легко видеть, что если F(x) первообразная функции для функции f(x), то функция (F(x)+C) тоже является первообразной для функции f(x), так как.
Опр.
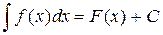 Если функция F(x) является первообразной для функции f(x), то выражение F(x)+C называется неопределенным интегралом от функции f(x) и обозначается символом
Если функция F(x) является первообразной для функции f(x), то выражение F(x)+C называется неопределенным интегралом от функции f(x) и обозначается символом
Функция F(x) называется подынтегральной функцией, f(x)dx –подынтегральным выражением.
Нахождение первообразной для данной функции f(x) называется интегрированием.