
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Непосредственное интегрирование.
|
|
Пользуясь таблицей интегралов и различными алгебраическими или трансцендентными преобразованиями подынтегральных функций можно вычислить многие интегралы.
Например:
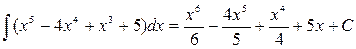 |
1.
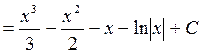
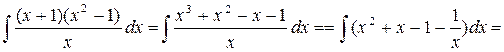 2.
2.
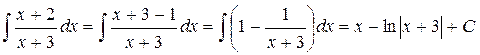 |
3.
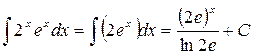 |
4.
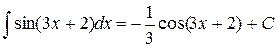 |
5.
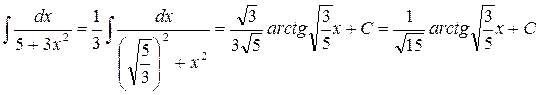 |
6.
 |
7.
Интегрирование методом подстановки.
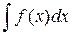 |
Пусть требуется найти интеграл
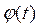
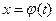 Заменим переменную в подынтегральном выражении, положив вместе где непрерывная вместе со своими производными функциями. Получим
Заменим переменную в подынтегральном выражении, положив вместе где непрерывная вместе со своими производными функциями. Получим
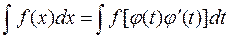 |
После интегрирования по переменной t перейдем к прежней переменной x, вновь воспользовавшись формулой x=j(t)
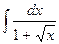 |
Например

Сделаем замену переменной, положив, тогда интеграл примет вид
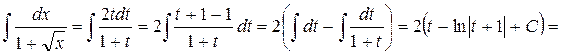 | |||
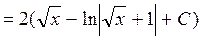 |
На практике чаще всего удобнее применять замену не в виде
x=j(t), а в виде t=j(x).
Покажем это на примерах:
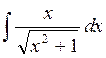 |
1.Найти
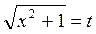 |
Положим, отсюда выразим х и найдем dx
 |
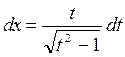 |
,
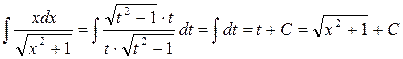
Тогда
 |
2.
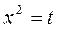 | |||
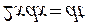 |
Полагаем, тогда
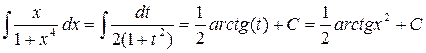 |
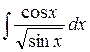 3.
3.
Положим sin(x)=t тогда cos(x)dx=dt
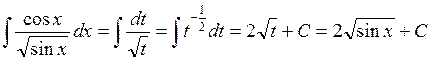 |