Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Интегрирование рациональных функций
|
|
Из высшей алгебры известно, что всякую рациональную функцию можно представить в виде рациональной дроби, т. е. двух многочленов
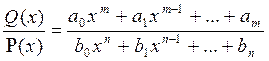 |
Рациональная дробь называется правильной, если степень числителя меньше степени полинома знаменателя.(m< n)
Рациональная дробь называется неправильной, если степень числителя больше или равна степени знаменателя (m³ n)
Если дробь неправильная, то разделив числитель на знаменатель по правилу деления многочленов, можно представить данную дробь в виде суммы многочлена и правильной дроби.
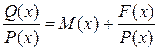 |
 |
Здесь M(x)- многочлен, правильная дробь
Так как интегрирование многочленов проводится непосредственно и не вызывает затруднений, то в дальнейшем все наши рассуждения относительно интегрирования рациональных функций будут относится к правильным рациональным дробям.
Правильные дроби вида:
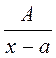 |
I.
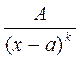 |
II.
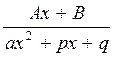 | |||
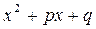 | |||
III. (не имеет действительных корней)
Называются простейшими дробями.
Интегрирование простейших дробей I, II, III типов нами уже было рассмотрено ранее.
Теорема

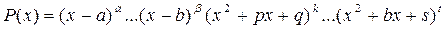 Если знаменатель правильной рациональной дроби разложен на множители:
Если знаменатель правильной рациональной дроби разложен на множители:
, то дробь
может быть представлена в виде суммы простейших дробей
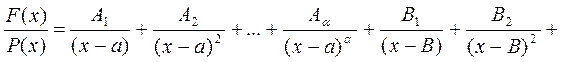 | ||||||
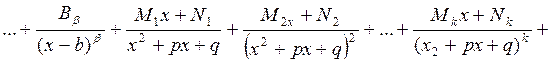 | ||||||
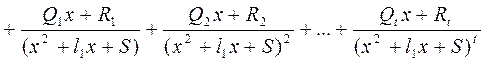 | ||||||
 |
 Для определения коэффициентов применяют метод неопределенных коэффициентов. Сущность метода состоит в следущем:
Для определения коэффициентов применяют метод неопределенных коэффициентов. Сущность метода состоит в следущем:
В правой части разложения простейшие дроби приводим к общему знаменателю, которым является многочлен P(x),
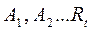 после чего знаменатель P(x) в левой и правой частях равенства отбрасываем. Получаем тождество, в левой части которого стоит многочлен F(x), а в правой многочлен содержащий неопределенные коэффициенты
после чего знаменатель P(x) в левой и правой частях равенства отбрасываем. Получаем тождество, в левой части которого стоит многочлен F(x), а в правой многочлен содержащий неопределенные коэффициенты
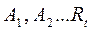 Приравнивая коэффициенты при одинаковых степенях получаем систему уравнений относительно искомых коэффициентов
Приравнивая коэффициенты при одинаковых степенях получаем систему уравнений относительно искомых коэффициентов
Например:
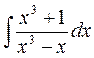 |
Найти интеграл
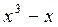
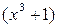 Подынтегральная дробь неправильная. Поэтому надо сначала выделить целую часть. Для этого поделим многочлен на многочлен и данную дробь представим в виде суммы многочлена и правильной дроби:
Подынтегральная дробь неправильная. Поэтому надо сначала выделить целую часть. Для этого поделим многочлен на многочлен и данную дробь представим в виде суммы многочлена и правильной дроби:
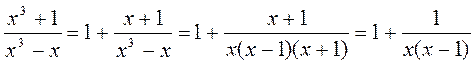 Напишем разложение
Напишем разложение
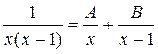
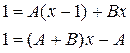 Приводим к общему знаменателю, и отбросив его, получаем
Приводим к общему знаменателю, и отбросив его, получаем
Приравнивая коэффициенты при одинаковых степенях, получаем систему
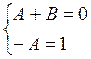
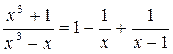 Отсюда A= -1, B=1
Отсюда A= -1, B=1
Окончательно имеем
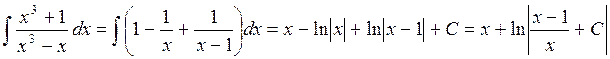 Следовательно
Следовательно
Пример 2
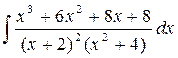 |
Напишем разложение:
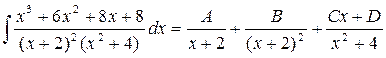 |
Приводим его к общему знаменателю и отбросив его, получаем
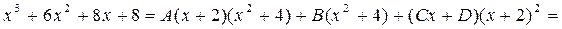
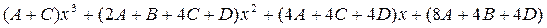 |
Приравнивая коэффициенты при одинаковых степенях получаем систему
A+C=1
2A+B+4C+D=6
4A+4C+4D=8
8A+4B+4D=8
Отсюда A=0, B=1, C=1, D=1
Тогда интеграл принимает вид