
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Интегрирование по частям. Формула интегрирования по частям имеет вид
|
|
Формула интегрирования по частям имеет вид
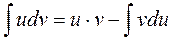 |
Справедливость формулы вытекает из того факта, что
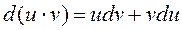 | |||
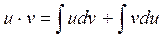 |
Отсюда, интегрируя получаем
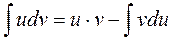 |
Откуда
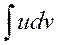 |
Формула интегрирования по частям сводит вычисление интеграла
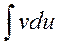 К вычислению интеграла. Поэтому метод интегрирования
К вычислению интеграла. Поэтому метод интегрирования
по частям применяют тогда, когда подынтегральное выражение представляет произведение двух дифференцируемых функций, причем производная от одной из функций, проще, чем заданная функция.
Например:
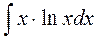 |
1.
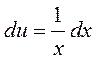 | |||
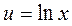 | |||
тогда
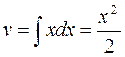 | |||
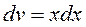 | |||
полагаем
 следовательно
следовательно
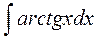 |
2.
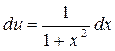 |
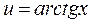 тогда
тогда
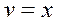
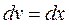 полагаем
полагаем
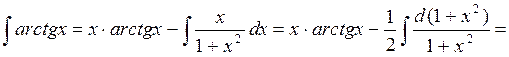 следовательно
следовательно
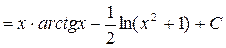 | ||
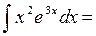 |
3.
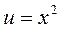 | |||
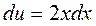 |
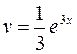
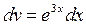 тогда
тогда
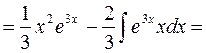 |
Применим формулу интегрирования по частям повторно:
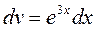 | 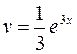 | ||
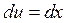
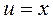 |
Полагаем
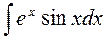 |
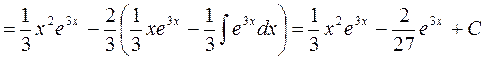
4.
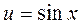 | |||
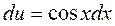 | |||
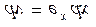
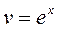 тогда
тогда
полагаем
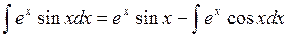 |
Следовательно
Интеграл правой части снова берем по частям
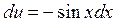 Полагаем
Полагаем
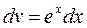
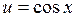 Тогда
Тогда
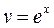 |
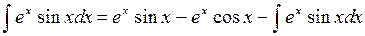 |
Следовательно
Следовательно
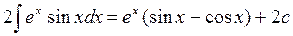 |
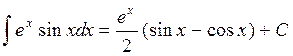
Откуда