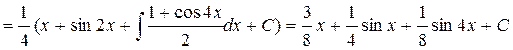Интегрирование тригонометрических функций

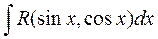
Пусть требуется найти интеграл вида

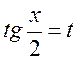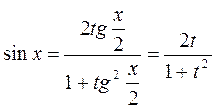Применим подстановку тогда

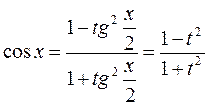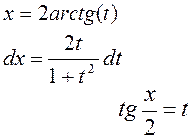Подстановка, носит название универсальной

тригонометрической подстановки; она сводит вычисление интеграла от тригонометрических функций к интегрированию рациональных выражений.

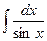Например:

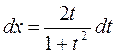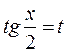Обозначим тогда

Тогда

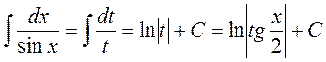
3. Интегралы от степеней тригонометрических функций

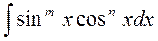, где m и n –действительные числа

а) Пусть m и n –действительные числа и по крайней мере одно из них положительное, нечетное.

Пусть например n=2p+1 тогда подынтегральная функция может быть записана в виде

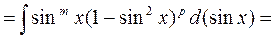Обозначим sin x = t

=

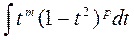Вычисление интеграла свелось к интегрированию рациональной функции

Пример 1:

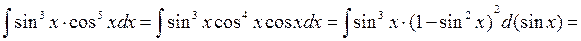sin x = t

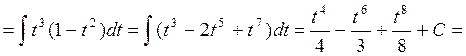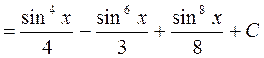Пример 2:

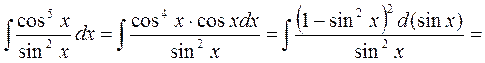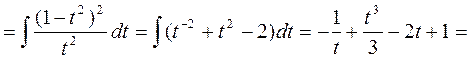
sin x = t

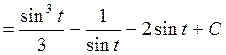
б) Пусть m и n действительные положительные четные числа (m=2p, n=2q), тогда интегрирование тригонометрических функций может быть сведено к интегрированию рациональных функций. Запишем, известные из тригонометрии формулы:

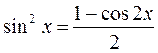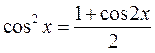И подставляем их в подынтегральное выражение

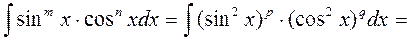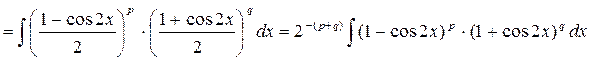Далее возведем двучлены в указанные степени, получим вновь четные и нечетные степени синуса и косинуса. Нечетные степени проинтегрируем как указано в пункте а), четные степени снова понизим по формулам «четных степеней».

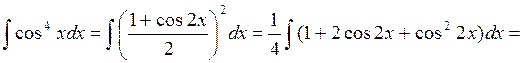
Например: