Интегрирование некоторых иррациональных выражений.

Интегрирование иррациональных выражений, вообще говоря, предствляет большую трудность.

Многие интегралы от иррациональных функций не выражаются через элементарные функции. Поэтому мы рассмотрим только некоторые частные случаи, когда заменой переменных можно от интеграла от иррациональной функции. Поэтому мы рассмотрим только некоторые частные случаи, когда заменой переменных можно перейти от интеграла от иррациональной функции перейти к интегрированию рациональных выражений.

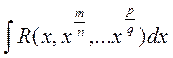
1.Рассмотрим интеграл вида

где R-рациональная функция, m, n, … p, q –целые числа

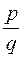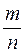Пусть к-общий знаменатель дробей …

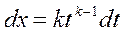
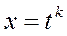Применим подстановку

Тогда каждая дробная степень выразится через целую степень t и иррациональная функция преобразуется в рациональную

Например

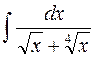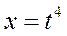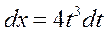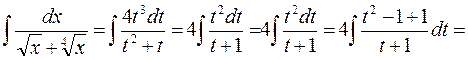Применим подстановку

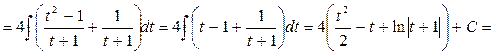2. Интегралы вида

вычисляются с помощью подстановки

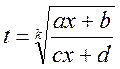
где k-наименьшее общее кратное чисел n…q

Например:

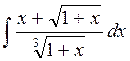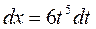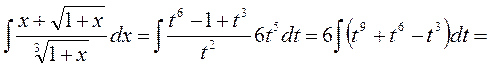Обозначим тогда