
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Теоретичні відомості. Поведінка великого класу технічних і фізичних систем, а також багатьох природних явищ досліджуються методами математичного моделювання і
|
|
Поведінка великого класу технічних і фізичних систем, а також багатьох природних явищ досліджуються методами математичного моделювання і, зокрема, із використанням подання їх у вигляді звичайних диференційних рівнянь (ЗДР).
У загальному випадку ЗДР першого порядку має вигляд:
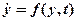 , (1.1)
, (1.1)
де f ‑ функція, t ‑ незалежна змінна (вважати, що t ‑ це час).
Для моделювання поведінки системи необхідно вирішити це рівняння, тобто одержати y (t).
Найбільш поширеним підходом до одержання розв'язання ЗДР є його чисельне інтегрування на комп’ютерах. Одним із найпростіших методів чисельного інтегрування є метод прямокутників (Ейлера), що реалізується за допомогою рекурентного співвідношення
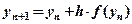 , (1.2)
, (1.2)
де yn – значення змінної y на n -ому кроку, h – крок інтегрування, отриманий шляхом ділення часової області інтегрування на рівні інтервали.
На практиці для чисельного інтегрування ЗДР широко застосовується метод Рунге-Кутта четвертого порядку:
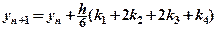 ,
,
 , (1.3)
, (1.3)
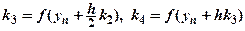 .
.
Відповідно до наведених співвідношень, на кожному кроці інтегрування проводиться чотири оцінки yn, а потім обчислюється їхнє середнє зважене значення. Глобальна похибка методу Рунге-Кутта четвертого порядку дорівнює O (h 4).